时序分割：U-TAE、TSViT、UTS-Former

本文内容来源于网络博客及GPT生成内容，作者并未详细阅读论文原文

U-TAE

1. 论文信息

属性	详细信息
标题	🔬 Panoptic segmentation of satellite image time series with convolutional temporal attention networks 🔬 基于卷积时空注意力网络的卫星图像时序全景分割
会议	📚 Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) 🏆 CCF-A
日期	⏲️ 2021
作者	👨‍🔬 Vivien Sainte Fare Garnot

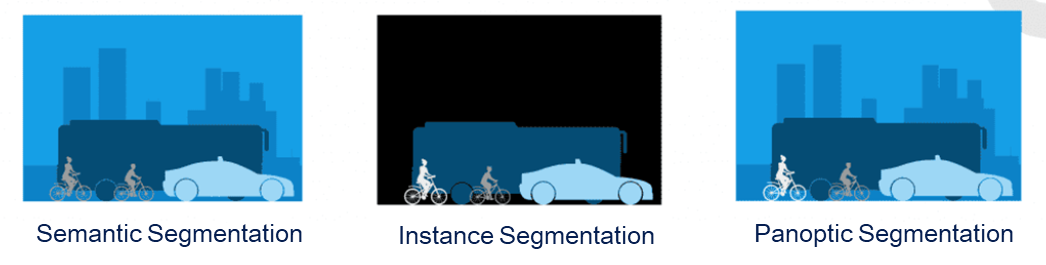
该论文的主要工作为提出适用于 卫星影像时序序列 | SITS 的全景分割方法，以及发布全景标注数据集（PASTIS）。在深入模型结构之前，我们不妨先了解目前 像素级密集预测 | dense predict 任务中的典型场景。总体上，这些任务可以分为三类：语义分割、实例分割、全景分割。关于这些任务的详细讲解可以参考「语义分割、实例分割、全景分割的区别 - huarzail」与「全景分割（CVPR 2019） - 77wpa」这两篇博客，这里我就简要总结一下这些任务：

语义分割（semantic segmentation）：对图像中每个像素进行类别预测，输出一张完整的语义类别图，但不区分同类目标的不同实例。
实例分割（instance segmentation）：在语义分割的基础上，为图中 可数对象 | thing 输出 类别标签 与 实例ID ，但对 不可数目标 | stuff 不进行处理。
全景分割（panoptic segmentation）：将语义分割和实例分割统一到同一框架下，为可数对象给出 类别标签 和 实例ID ，对不可数目标仅给出 类别标签 。

以街景影像为例，这里的thing实际上是我们在训练时关注的可数对象（如人、车等可数对象），而stuff则指哪些我们不关心实例数量的类别（如天空、道路等不可数对象），对于这些像素，我们只需要对其语义类别标注即可。需要注意的是，某些stuff类别（如建筑）理论上也可以划分为若干实例，但由于任务设定我们将其视为stuff处理。

01bf58f6e8d1b96ff968a194afcd6b6c

语义分割、实例分割与全景分割

在常规的图像语义分割任务中，输入数据通常表示为 $C_\text{in}\times H\times W$ ，模型只需输出一个尺寸为 $C_\text{out}\times H\times W$ 的特征图，即可完成像素级的分类预测。然而，当处理 SITS 数据时，除了光谱/通道维度 ( $C$ )，还需要显式区分 时间维度 ( $T$ )。如果仅将时间序列简单拼接在通道维度上，往往难以捕获序列间的动态演化特征。

因此，更常见的做法是将原始数据组织为 $X\in \mathbb{R}^{T\times C_\text{in}\times H\times W}$ 的输入，其中， $T$ 表示时间步数， $C_\text{in}$ 表示输入光谱通道数。这样，模型能够同时感知时间序列信息与空间/光谱特征。在输出端，通常依旧需要得到一个尺寸为 $C_\text{out}\times H\times W$ 的特征图，用于后续任务。

该论文提出的模型架构也遵从上述SITS数据组织范式，其先使用时空编码模块（U-TAE）对时序数据进行特征提取得到形如 $C_\text{out}\times H\times W$ 的特征图，然后再使用全景分割模块（PaPs）实现后续的全景分割任务。同样，这篇论文在网上也有博客「解读 - 小菜鸟」对其解读。

2. 时空编码

时空编码模型名为UTAE，即 带时间注意力编码器的UNet 。其模型结构如下：

figure 1.2. U-TAE时空编码模块

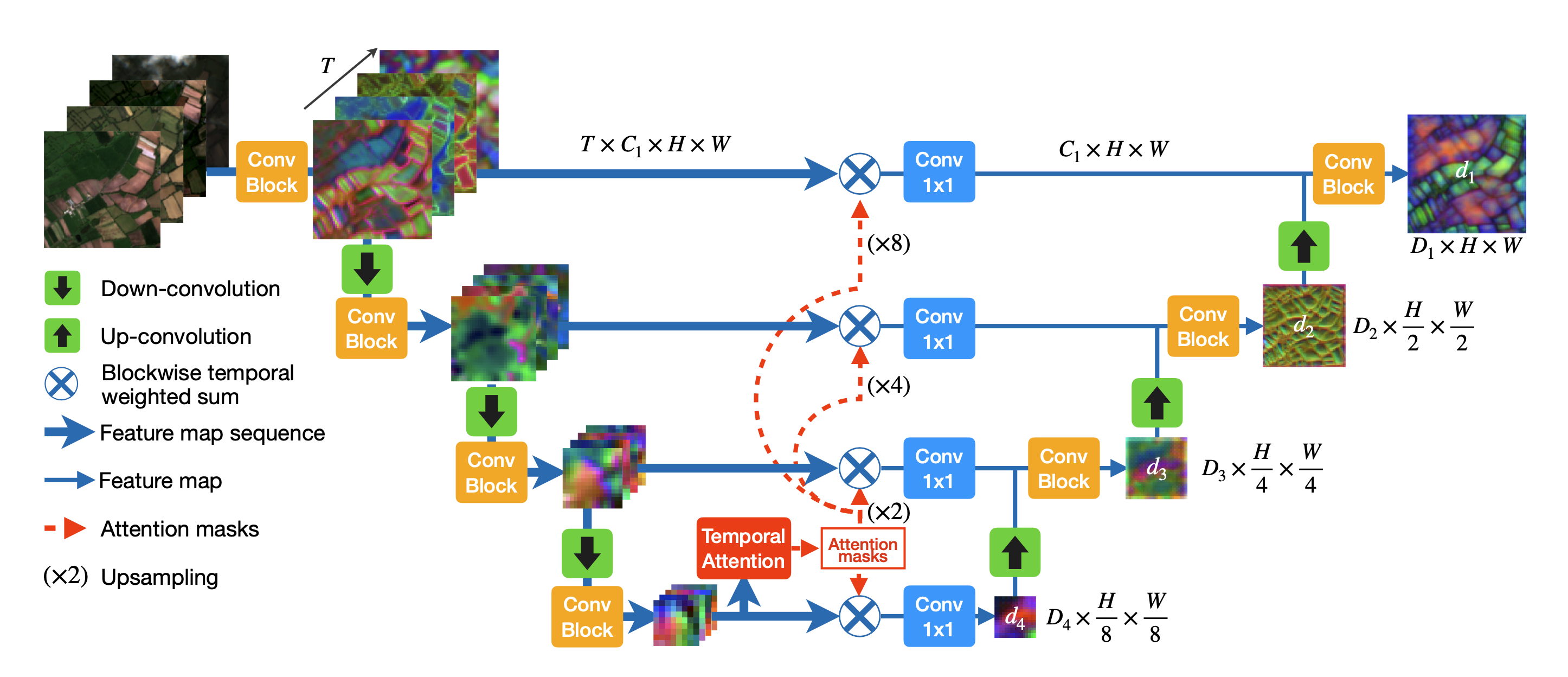
对于像UTAE这类面向时序影像的 密集预测模型，一个核心设计要点在于：如何消除特征张量中的时间维度。具体而言，模型需要将跨时间序列的特征压缩或聚合，使得输出特征图中每个像素最终都由一个一维向量表示。通过这种方式，我们可以将原本的 时序密集预测问题 转化为一个 常规密集预测问题，从而当前模型能够直接借鉴成熟的密集预测模型来完成余下工作。

🎯 归一化

在深入UTAE模型结构前，我们来了解一下模型中常用的归一化操作。

首先，归一化操作是在做什么呢？给定某层的输出 $x$ ，归一化操作就是用某个轴上的均值和方差把输入数据标准化到标准正态分布（ $\hat{x} \sim \mathcal{N}(0, 1)$ ），然后再用可学习的缩放和平移参数 $\gamma$ 、 $\beta$ 复原尺度和偏置（bias）。

\begin{align*} \hat{x} = \frac{x-\mu}{\sqrt{\sigma^2+\varepsilon}},\;\;y=\gamma\hat{x}+\beta \end{align*}

模型引入归一化操作通常是为了训练数据时把数值范围压缩到可控的区间，使得模型在训练时能设置更大学习率，且模型梯度更加稳定，能快速收敛^GPT。

模型中常有如下几类归一化方法，下面我们来详细了解一下它们。

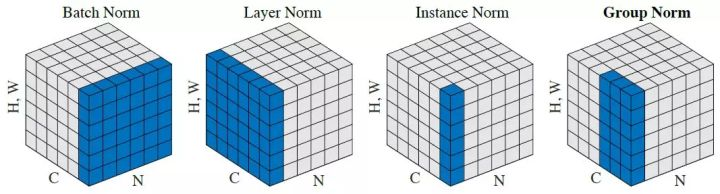
激活（中间特征）| activations 归一化分类

在详细介绍这些 归一化 方法前，我们先来逐步了解一下批 | Batch 这一概念：

在深度学习中，训练模型的核心目标是通过梯度下降法寻找期望的最优参数解。通常，我们会在训练开始时对模型参数进行初始化，然后通过反向传播算法根据梯度更新参数。理想情况下，如果我们能够获得模型在整个数据分布上的所有输出误差，就能计算出真实梯度（ $\nabla \mathcal{L}(\theta) = \mathbb{E}_{x \sim \mathcal{D}}(\nabla l(x;\theta))$ ，其中 $\mathcal{D}$ 表示输入数据的真实分布， $\theta$ 表示模型参数），并据此进行精确的参数更新。

然而，实际情况并不允许我们访问整个数据分布。模型只能在有限的训练数据（训练集）上进行学习，因此我们必须使用小批量样本来估计梯度（无偏估计）。由此我们便为模型训练引入了批这一概念：通过在每次迭代中使用一个小样本集合计算梯度（ $g_B$ ），我们既能降低计算开销，又能有效逼近真实梯度，从而实现高效的模型训练。

\begin{align*} g_B = \frac{1}{B}\sum_{i=1}^B\nabla l(x_i;\theta),\;\;\mathbb{E}[g_B] = \nabla \mathcal{L}(\theta) \end{align*}

在深度学习模型训练时，我们通常将数据分为训练集 | train 、验证集 | valid 、测试集 | test 三个部分分别用于模型训练的各个阶段：

🔹 训练集用于训练模型参数，整个前向传播和反向传播都是使用的训练集。

🔹 验证集用于在模型训练时检查模型的 泛化能力 ，我们通常在训练时，定期在验证集上评估模型，常用于对模型进行超参数调参（模型超参数、Batch size、Epoch等）以及停止模型训练。

🔹 测试集用于最终评估模型的泛化性能，不参与模型任何训练。

批大小 | batch_size 的设置也是一个值得研究的课题。在实际训练中，我们通常采用 mini-batch 的方式进行前向和反向传播，而不是使用全数据（full-batch）或者逐样本（batch_size=1）。原因在于：

如果批大小设置过小，梯度估计的方差较大，训练过程噪声大，模型收敛会出现抖动；
如果批大小过大，虽然梯度噪声减少，但训练的边际收益递减，同时显存占用和分布式训练时的通信开销都会显著增加。

此外，批大小还会从如下角度影响训练^GPT：

🔹 稳定性与学习率：大批量允许更大学习率；常见经验则是线性缩放法则：当批大小从 $B$ 变为 $kB$ 时，将学习率从 $\eta$ 调到 $k\eta$ （配合 warmup 更稳）。也有人用 $\sqrt{k}$ 缩放，噪声更接近不变。

🔹 数值与混合精度：大批量常配合 混合精度（AMP）与梯度缩放（loss scaling），以避免下溢。

🔹 泛化：小批量产生的“梯度噪声”像一种隐式正则化，经验上常更容易得到平坦解、泛化更好；大批量可能出现“泛化间隙”，可用更强正则（权重衰减、数据增强、长 warmup、优化器如 LARS/LAMB ）缓解。

顾名思义，批归一化 | Batch Norm 就是对一个批次中的元素进行归一化操作。在不同的任务场景中，归一化的对象和维度会根据数据结构调整：

在图像处理任务中，输入数据通常以(batch_size, channels, height, width)的形式存在。此时批归一化会针对每个通道维度上的分布进行归一化操作。
在自然语言处理 或 结构化数据任务 中，输入特征通常为(batch_size, feature_dim)的二维矩阵，批归一化则会对每个特征维度（即feature_dim的每个维度）上的分布进行归一化操作。

需要注意的是，模型在训练与推理时的批归一化 的统计量的来源不同。

训练时，BN会根据当前批次数据计算均值和方差，并基于这两个统计量完成归一化。同时，为了让模型在推理时能使用更贴近全局数据的统计量，训练过程中会通过 指数滑动平均 | EMA 持续累积批次统计量，得到全局均值和全局方差的近似值。

\begin{align*} \mu_{\text{running}} &= \alpha\cdot \mu_{\text{running}} + (1-\alpha)\cdot \mu_B\cdot\sigma_{\text{running}}^2 \\\\ \sigma_{\text{running}}^2 &= \alpha\cdot \sigma_{\text{running}}^2 + (1-\alpha)\cdot \sigma_B^2 \end{align*}

其中， $\alpha$ 为衰减系数（通常取 $0.9$ 或 $0.99$ ），用于平衡历史统计量和当前批次统计量的权重。

模型训练显然是一个异步过程，我们只有完成一个 batch 的前向传播+反向传播后，才能进行下一个 batch 的计算。当我们引入多卡分布计算时，实际上是将一个 global batch 均匀分配到各个计算卡上计算，其中的一个子批次（local batch）的大小为local_batch_size = global_batch_size / num_gpus。而BN要求在训练时计算一个 global batch 内训练数据的均值和方差，这就需要我们在训练时，把所有 GPU 上的 local batch 的统计量聚合起来，再算全局的均值和方差。

其他 归一化 方法的特点以及使用常见如下表所示：

归一化方法	常用场景	优点	缺点 / 注意事项
BatchNorm	CNN（大 batch 训练）	缓解内部协变量偏移，加速收敛，具有轻微正则化效果	小 batch 时统计不稳定；对 RNN 或序列模型不太适用
LayerNorm	Transformer / NLP / ViT	对 batch 尺寸无依赖，适合堆叠深层网络，序列模型中稳定性高	对 CNN 的空间特征处理效果不一定理想；增加计算开销
InstanceNorm	风格迁移 / GAN	消除样本间风格差异，使生成图像风格统一	可能破坏全局统计信息，损失图像内容一致性
GroupNorm	小 batch CNN / 检测 / 分割	对 batch 尺寸不敏感，适合小 batch 或高分辨率输入，在 CNN 中稳定	需调节组数 G，计算稍高；对特征通道划分敏感

🪢 空间编/解码

在介绍UTAE空间编码器前，我们不妨先回忆一下UNet的编码器结构。UNet 通过卷积块+下采样实现对输入影像的多尺度特征提取。具体来说，第 $l$ 层卷积块会提取输入的特征信息，然后通过下采样操作将特征图尺寸减半，作为第 $l+1$ 层卷积块的输入，从而逐步捕捉更大感受野的空间信息。

UTAE处理的是SITS数据，其输入形式为 $X \in \mathbb{R}^{T \times C \times H \times W}$ ，其中 $T$ 表示时间步长， $C$ 为通道数， $H$ 和 $W$ 分别为空间高度和宽度。虽然输入数据与UNet不同，但在空间编码阶段，UTAE对每一个时间步 $t$ 的特征图进行的操作，本质上类似于UNet编码器中的卷积+下采样流程。也就是说，对于每个时间步，UTAE的空间编码器会提取局部空间特征，同时通过多层结构捕获更高层次的空间语义信息。论文采用如下公式描述这一过程：

\begin{gather*} e^l = [\mathcal{E}_l(e_t^{l-1})]_{t=0}^T\;\;\text{for}\;\;l\in [1,L] \end{gather*}

其中， $[\cdot]$ 表示沿时间维度的拼接操作， $e_t^{l-1} \in \mathbb{R}^{C_{l-1}\times H_{l-1}\times W_{l-1}}$ 表示时间步 $t$ 在第 $l-1$ 层的输出特征图（ $H_l = H/2^{l-1},\;W_l = W/2^{l-1}$ ）， $\mathcal{E}_l(\cdot)$ 表示第 $l$ 层空间编码器。

UTAE空间编码器的核心计算单元是DownConvBlock，其结构如下：

class DownConvBlock(TemporallyShareBlock):
  def forward(self, input):
    out = self.down(input)
    out = self.conv1(out)
    out = out + self.conv2(out)	# residual connect, not skip connect
    return out

需要注意的是，其中Conv组件的具体结构为：(Conv2D → GN → ReLU) $\times$ kernel_num，即UTAE空间编码器 组归一化 是在卷积单元中实现的。

由于UTAE的空间编码器是 以时间步 $t$ 为单位进行空间特征提取的，因此在跨层传递过程中，时间维度 $T$ 不发生变化。在实际实现中，作者采取了一个简洁的方式：UTAE会先将时间维度和批次维度展开到一起（input.view(b * t, c, h, w)），然后再经过DownConvBlock处理后还原到原维度（out = out.view(b, t, c, h, w)）。

📌 如果想深入理解实现细节，可以直接阅读 UTAE-paps - utae.py；

通过这种方式，UTAE能够在保持时间顺序信息的同时，对每个时间步的空间特征进行高效编码，为后续的时序建模提供富含空间语义的输入。最终第 $l$ 层输出的特征图尺寸为 $T\times C_l\times H_l\times W_l$ 。

由UTAE结构图可知，UTAE空间编码器的各尺度输出在经过时间编码后消除了时间维度，其尺寸变为 $C_l\times H_l\times W_l$ 。因此，UTAE空间解码器的实现则与UNet几乎一致，论文采用如下公式描述这一过程：

\begin{gather*} d^l = \mathcal{D}_l([\mathcal{D}_l^\text{up}(d^{l+1}), f^l])\;\;\text{for}\;\;l\in [1,L-1] \end{gather*}

其中， $[\cdot ]$ 表示按通道维度拼接。最终，经过UTAE空间编/解码器的处理，我们得到了尺寸为 $C_1\times H \times W$ 的特征图用于全景分割输入。

⌚️ 时间编码

UTAE的时间编码模块，本质上是通过注意力机制来对时序特征图进行信息聚合。相比传统方法，作者在两个方向上做了改进：

卷积循环UNet（CR-UNet）：UTAE 通过对最低分辨率的时序注意力掩码进行双线性插值，使得各尺度的编码器特征都能参与时序建模。

Convolutional-recurrent U-Net networks [41, 36, 28] only process the temporal dimension of the lowest resolution feature map with a temporal encoder. The rest of the skip connections are collapsed with a simple temporal average. This prevents the extraction of spatially adaptive and parcel-specific temporal patterns at higher resolutions.

卷积循环U-Net网络[41, 36, 28]仅通过时间编码器处理最低分辨率特征图的时间维度。其余的跳跃连接通过简单的时间平均（即使用求均值的方法压缩时间维度）进行合并。这阻止了在更高分辨率下提取空间自适应和地块特异性时间模式。
轻量级时间注意力编码器模块（Lightweight-Temporal Attention Encoder, L-TAE）：作者选择了 L-TAE 作为时间编码器，同时借助通道分组策略提升计算效率与特征对齐稳定性。

Based on its performance and computational efficiency, we choose the Lightweight-Temporal Attention Encoder(L-TAE) [10] to handle the temporal dimension. The L-TAE is a simplified multi-head self-attention network [44]in which the attention masks are directly applied to the input sequence of vectors instead of predicted values. Additionally, the L-TAE implements a channel grouping strategy similar to Group Normalization [49].

基于其性能和计算效率，我们选择轻量级时空注意力编码器（L-TAE）[10]来处理时空维度。L-TAE是一种简化的多头自注意力网络[44]，其中注意力掩码直接应用于向量输入序列，而非预测值。此外，L-TAE实现了与组归一化[49]类似的通道分组策略。

下面我们通过论文中相关公式，来详细了解一下模型的这部分计算过程：

\begin{gather*} a^{L,1},\cdots,a^{L,G} = \operatorname{LTAE}(e^L),\; \text{applied pixelwise.} \tag{1}\\\\ a^{l,g} = \operatorname{BiLinear(a^{L,g}, (T\times H_l\times W_l))} \tag{2}\\\\ f^l = \operatorname{Conv}_{1\times 1}^l\left( \left[ \sum_{t=1}^Ta_t^{l,g} \odot e_t^{l,g} \right]_{g=1}^G \right)\tag{3} \end{gather*}

公式 $(1)$ 中，UTAE首先在通道维度上进行分组，然后在每个分组内通过 L-TAE 计算时序注意力分数。这里得到了最低分辨率时序权重矩阵 $a^{L,g} \in \mathbb{R}^{T\times H_L\times W_L}$ ，其取值范围为 $[0,1]$ 。从 $a^{L,g}$ 的形状不难看出，同一个分组内的所有通道共享同一组时序权重矩阵，这种设计可以在保证计算效率的同时，避免对单个通道过度独立建模。

既然UTAE的时间编码和空间编码中都是使用的 分组策略 进行计算，这里也引用一下GPT对此的解答：

🔹 组归一化

在遥感任务中，输入数据通常是高分辨率、多时间步的影像序列。如果直接用批归一化，当 batch_size 太小时，统计量就会出现不稳定的问题。而实例归一化在每个样本、每个通道上独立归一化，虽然避免了 BN 的问题，但可能会过度消除跨空间的对比信息，对语义特征提取不够友好。

组归一化在通道维度分组后进行归一化，即不依赖 batch_size ，适合小 batch 训练，又保留了一定通道间的统计特征，相比 IN 更能保留判别性信息。

🔹 L-TAE分组策略

由于在UTAE空间编码阶段，卷积特征已经通过 GN 归一化，如果在 L-TAE 中改用其他归一化方式，会导致特征分布不一致，使得跨模块的特征对齐变差。使用相同的 GN分组策略，可以保证特征的统计性质在 空间编码 → 时序编码 的过程中保持稳定。

公式 $(2)$ 表示将初始时序权重矩阵与各尺度时序特征图进行尺度对齐操作，保证每一层次时序特征图都能使用时序加权矩阵进行信息聚合操作。

公式 $(3)$ 中，模型利用时序权重矩阵对时序特征进行加权聚合。

其中， $\odot$ 表示逐元素相乘（支持通道广播）。也就是说，在某个时刻 $t$ ，特征图通道向量的每个空间位置都会与注意力权重（ $[0,1]$ 范围数值）对应相乘；
$\sum_{t=1}^T$ 表示对时间维度求和，从而得到时序聚合后的空间特征；
$[\cdot]_{g=1}^G$ 表示将不同分组的结果在通道维度拼接，得到一个形如 $C_\text{in} \times H_l \times W_l$ 的张量。

最后，模型在拼接后的特征上施加一个1×1 Conv2D，实现跨分组信息的融合，并生成第 $l$ 层的编码器跳跃连接输入。

接下来，我们来看看时间编码中的 L-TAE 模块，这是作者在另一篇论文中提出的一个轻量级时间注意力机制。下面我们通过源码来理解其核心结构与计算逻辑：

class LTAE2d(nn.Module):
    def __init__(
        self,
        in_channels=128,
        n_head=16,
        d_k=4,
        mlp=[256, 128],
        dropout=0.2,
        d_model=256,
        T=1000,
        return_att=False,
        positional_encoding=True,
    ):
        pass

    def forward(self, x, batch_positions=None, pad_mask=None, return_comp=False):
        sz_b, seq_len, d, h, w = x.shape
        
        # 1) 处理 pad_mask，使其扩展到空间维度
        if pad_mask is not None:
            pad_mask = (
                pad_mask.unsqueeze(-1)
                .repeat((1, 1, h))
                .unsqueeze(-1)
                .repeat((1, 1, 1, w))
            )  # (B,T,H,W)
            pad_mask = (
                pad_mask.permute(0, 2, 3, 1).contiguous().view(sz_b * h * w, seq_len)
            )
        
        # 2) 展开空间维度, 形状变化: (B,T,C,H,W) → (B·H·W,T,C), 记 N=B·H·W
        out = x.permute(0, 3, 4, 1, 2).contiguous().view(sz_b * h * w, seq_len, d)
        
        # 3) 输入归一化: GroupNorm(num_groups=n_head, num_channels=in_channels)
        # 这里先把形状变为 (N,C,T) 以便 GroupNorm , 然后再还原为 (N,T,C)
        out = self.in_norm(out.permute(0, 2, 1)).permute(0, 2, 1)

        # 4) (可选) 使用Conv1D实现通道投影: C → d_model
        # 这里的形状变化同上, 最终输出的尺寸为 (N,T,C|d_model)
        if self.inconv is not None:
            out = self.inconv(out.permute(0, 2, 1)).permute(0, 2, 1)

        # 5) (可选) 加入位置编码(时间编码)
        if self.positional_encoder is not None:
            # 每个Batch都有一个时间序列表示，各影像的时间刻
            # 这操作只是把一个值(T)转换为了一个矩阵(T,H,W), 让每幅影像的每个位置都有时间刻对应
            # 时间刻的具体值可能是 *序列号* ，也可能 *DayOfYear* 
            bp = (
                batch_positions.unsqueeze(-1)	# (B, T) → (B, T, 1)
                .repeat((1, 1, h))
                .unsqueeze(-1)
                .repeat((1, 1, 1, w))
            )  # (B,T,H,W)
            bp = bp.permute(0, 2, 3, 1).contiguous().view(sz_b * h * w, seq_len) # (N,T)
            out = out + self.positional_encoder(bp) # (N,T,d_model)

        # 6) 多头注意力
        # 输入 out: (N,T,d_model)
        # 输出 out: (Head,N,d_v), 其中 d_v = d_model/Head
        # 输出 attn: (Head,N,T)，表示每个 head 对时间维度的注意力分布
        out, attn = self.attention_heads(out, pad_mask=pad_mask)
        
        # 这里的Q时模型中的可学习参数，每一个Head一个，不依赖外部输入:
        # 	self.Q = nn.Parameter(torch.zeros((n_head, d_k))) 
        # 	其形状为(Head, d_k)
        # 在实际计算时，UTAE会复制N个Q构成矩阵, 以便快速计算
        # 	q = torch.stack([self.Q for _ in range(sz_b)],dim=1).view(-1, d_k)
        # 	其形状为(Head·N, d_k)
        # 同样, k,v也会进行将Batch和Head维度展开，以便快速计算
        # 	k = self.fc1_k(v).view(sz_b, seq_len, n_head, d_k)
        # 	k = k.permute(2, 0, 1, 3).contiguous().view(-1, seq_len, d_k)
        # 	其形状为(Head·N, T, d_k)
        
        # 	v = torch.stack(v.split(v.shape[-1] // n_head, dim=-1)).view(n_head * sz_b, seq_len, -1)
        # 	其形状为(Head·N, T, d_v), 其中 d_v = d_in/Head
        
        # 然后我们便可得到注意力分数矩阵 attn, 其形状为 (Head·N, 1, T)
        
        # 7) 最低分辨率时序特征图特征聚合结果
        # 这里的 out 实际上就是使用 attn 对最低分辨率时序特征图进行时间维度信息聚合的结果
        # 在UTAE实现代码中，不需要再次对该分辨率做聚合
        out = (
            out.permute(1, 0, 2).contiguous().view(sz_b * h * w, -1)
        )  # Concatenate heads
        out = self.dropout(self.mlp(out))
        out = self.out_norm(out) if self.out_norm is not None else out
        out = out.view(sz_b, h, w, -1).permute(0, 3, 1, 2) # (B,C_out,H,W)

        # 7) 重塑注意力权重矩阵为 (Head,B,T,H,W)
        attn = attn.view(self.n_head, sz_b, h, w, seq_len).permute(
            0, 1, 4, 2, 3
        )  # (Head,B,T,H,W)

        if self.return_att:
            return out, attn
        else:
            return out

从代码逻辑不难发现，LTAE实际上是基于注意力机制实现的，其计算流程大致如下：

空间展平：将输入影像在空间维度展开，把每个像素点的位置视为一个“序列样本”，这样输入由(B,T,C,H,W)转换为(N,T,C)，其中N = B·H·W。
归一化与通道投影：对时间维度上的特征做 组归一化，可选使用Conv1d投影到新的特征维度d_model。

时间位置编码：若启用，会为每个时间步加入位置编码，使模型具备 时间顺序感知能力 ：

class PositionalEncoder(nn.Module):
    def __init__(self, d, T=1000, repeat=None, offset=0):
        super(PositionalEncoder, self).__init__()
        # token向量维度, 这里实际上是 d_model // n_head
        self.d = d
        self.T = T
        # 支持重复维度, 可以把生成的正余弦编码重复拼接多份. 扩大到更高维度
        self.repeat = repeat
        # 对应经典Transformer位置编码的频率分母: 10000^{2i/d}
        # // 2操作确保偶数和奇数索引使用相同的频率基数
        self.denom = torch.pow(
            T, 2 * (torch.arange(offset, offset + d).float() // 2) / d
        )
        self.updated_location = False

    # 前向传播中输入的BP尺寸为: (N,T) 或 (B·H·W, T)
    # 在后续计算中将 N 视为 Batch_size
    # BP在模型训练时提供给utae, 然后再传给ltae和pe, 
    def forward(self, batch_positions):
        if not self.updated_location:
            self.denom = self.denom.to(batch_positions.device)
            self.updated_location = True
        # 位置编码计算核心部分: 
        # 1. batch_positions[:, :, None]给输入增加一个维度，形状变为 (B, T, 1)
        # 2. 除以self.denom得到不同频率的位置值，形状变为 (B, T, d)
        sinusoid_table = (
            batch_positions[:, :, None] / self.denom[None, None, :]
        )  # B x T x d
        sinusoid_table[:, :, 0::2] = torch.sin(sinusoid_table[:, :, 0::2])  # dim 2i
        sinusoid_table[:, :, 1::2] = torch.cos(sinusoid_table[:, :, 1::2])  # dim 2i+1

        # 如果设置了repeat参数，会将生成的位置编码在最后一个维度上重复拼接，扩展编码维度
        if self.repeat is not None:
            sinusoid_table = torch.cat(
                [sinusoid_table for _ in range(self.repeat)], dim=-1
            ) # B x T x d_model

        return sinusoid_table

需要注意的是，LTAE 使用的位置编码是在经典正弦余弦编码的基础上的改进版本。传统正弦余弦编码中，我们直接为每个 token 生成一个 $d_\text{model}$ 长度的位置编码，而该改进版本只需生成d = d_model // n_head维度的基础编码，通过重复拼接得到最终编码（仍为d_model维度），这样减少了存储和计算开销。

当我们根据序号生成对应的正弦余弦编码时，使用的可能是图像的 序列号 或者 一年中的天数 | DOY 。这里仅作猜测，具体实现还需阅读源码和 LTAE 原论文。

多头注意力计算：将输入序列作为 Key、Value 与可训练查询向量 Q 进行注意力计算。由于这里使用的是多头注意力，实际上LTAE是为每个头单独维护一个查询向量 Q 。

此外，在实现时 K 是原序列经线性变换（FC）后得到的新序列，而 V 则是对原序列的通道维度进行拆分而得到的。
信息聚合：利用得到的注意力权重在时间维度聚合每个像素点的时序特征，最终输出 (B,C,H,W) 的聚合特征图。

在理解 LTAE 的时间注意力机制时，可以将其中的查询向量 Q 与 ViT 的[CLS] token 做一个对比。二者在形式上虽然不同，但本质上都是通过为注意力机制引入可训练参数来完成全局聚合信息。

在 LTAE 中，查询向量 Q 对全空间位置共享，对每个空间位置的时序特征序列进行注意力权重计算，并用该权重信息聚合时序信息。换句话说，Q 并不是直接表征输入的一部分，而是充当了一个“全局探针”，帮助模型在不同时间片之间建立权重分布。而在 ViT 中，我们也是透过[CLS] token 观察输入特征序列，从而得到空间尺度的注意力权重矩阵（需重塑差值），并用于[CLS] token 与各 patch token 的信息聚合。

从注意力权重分布的角度来看，两者又有高度相似之处。在 ViT 中，常见的可视化方法是观察 [CLS]（记作 $e_0$ ）对其他 patch token（记作 $e_1, e_2, \dots, e_N$ ）的注意力权重，先得到一个尺寸为 $1\times N$ 的注意力向量，再重塑插值为 $H\times W$ 形状的权重矩阵；而LTAE 则为每个空间位置都计算一个 $1\times T$ 的注意力向量。两者本质上非常接近——都是在用一个序列外的查询向量，去查询序列的注意力分布情况。

此外，需要注意的是，ViT 的[CLS]是在输入阶段就引入的，并且与其他 token 一样需要位置编码，以保留顺序信息；而 LTAE 的 Q 则是模块内部的固定查询向量，不承担输入表征的职责，因此无需位置编码。

代码中实现实现的信息聚合方法有三种：

attn_group：将通道划分为Head组（同LTAE的组归一化分组），利用每个 head 的注意力权重对分组后的特征进行加权，最后拼接结果。这样保留了多头的多样性，输出 (B,C,H,W)。
attn_mean：对所有 head 的注意力权重在 head 维度上求平均，得到一个(B,T,H,W)的统一权重，再对输入序列特征加权聚合。
mean：不使用注意力，直接在时间维度取平均，作为最简单的 baseline 方法。

📖 这里就不过多介绍LTAE具体实现细节，进一步阅读可参考原论文：

属性	详细信息
标题	🔬 Lightweight Temporal Self-Attention for Classifying Satellite Image Time Series 🔬 轻量级时空自注意力机制在卫星图像时间序列分类中的应用
信息	👨‍🔬 Vivien Sainte Fare Garnot \| ⏲️ 2020

3. 其他

一般来说，在语义分割任务中，经过编码器—解码器结构提取和还原特征图之后，直接接入一个1×1 Conv2D就可以完成像素级的分类预测。但本文所研究的任务是 全景分割 。为此，作者在UTAE模块之后，引入了 PaPs（Parcels-as-Points） 模块，从而构建出端到端的全景分割框架。该模块的整体结构如图所示：

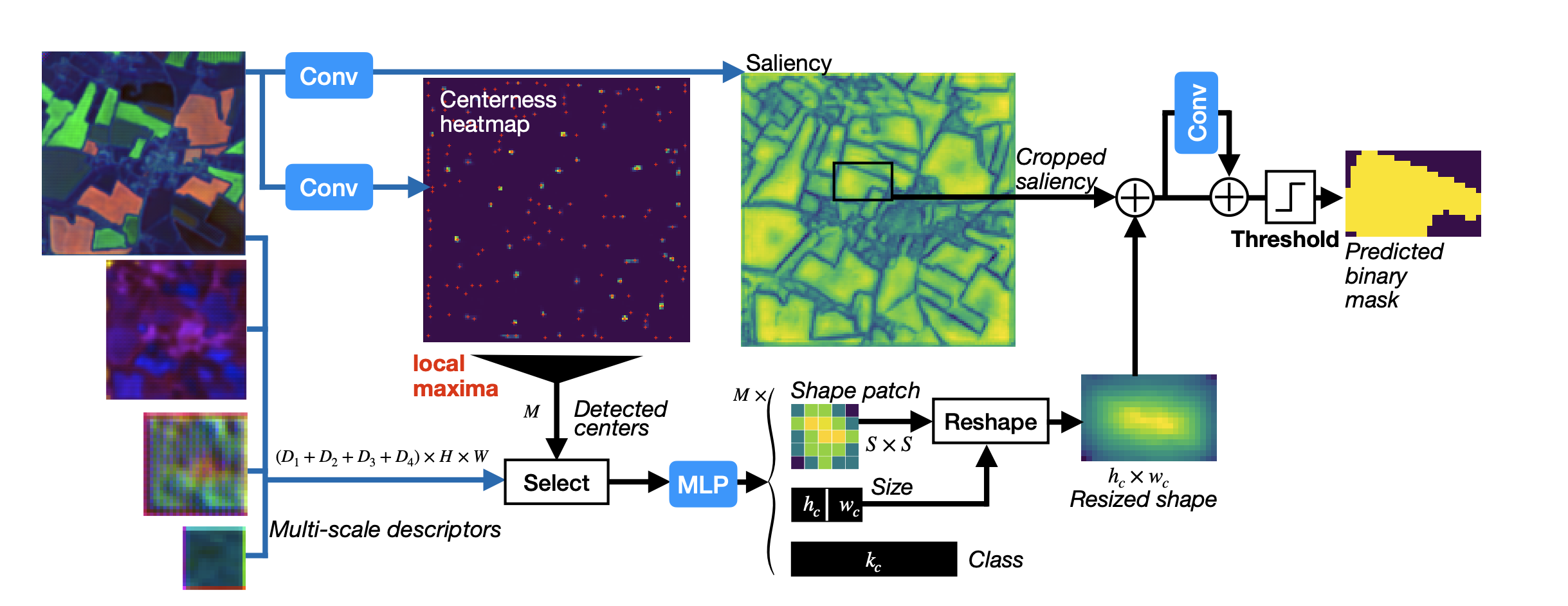
figure 1.4. PaPs全景分割

由图可知，PaPs 模块主要由 边界框位置/大小预测、地物边界预测、地物类型预测 等多个子模块组成。通过这些组件，PaPs 能够同时输出对象类别、边界框以及实例掩码，从而实现全景分割所要求的「语义 + 实例」的统一建模。在此就不对 PaPs 内部的具体 损失函数设计 与 实现细节 展开说明，若想详细了解可参考论文原文及模型源代码。

此外，论文使用了 UTAE 做了语义分割实验对比，实验结果如下：

table 1.1. UTAE在语义分割任务中与其他方法的对比实验，以及模块消融实现

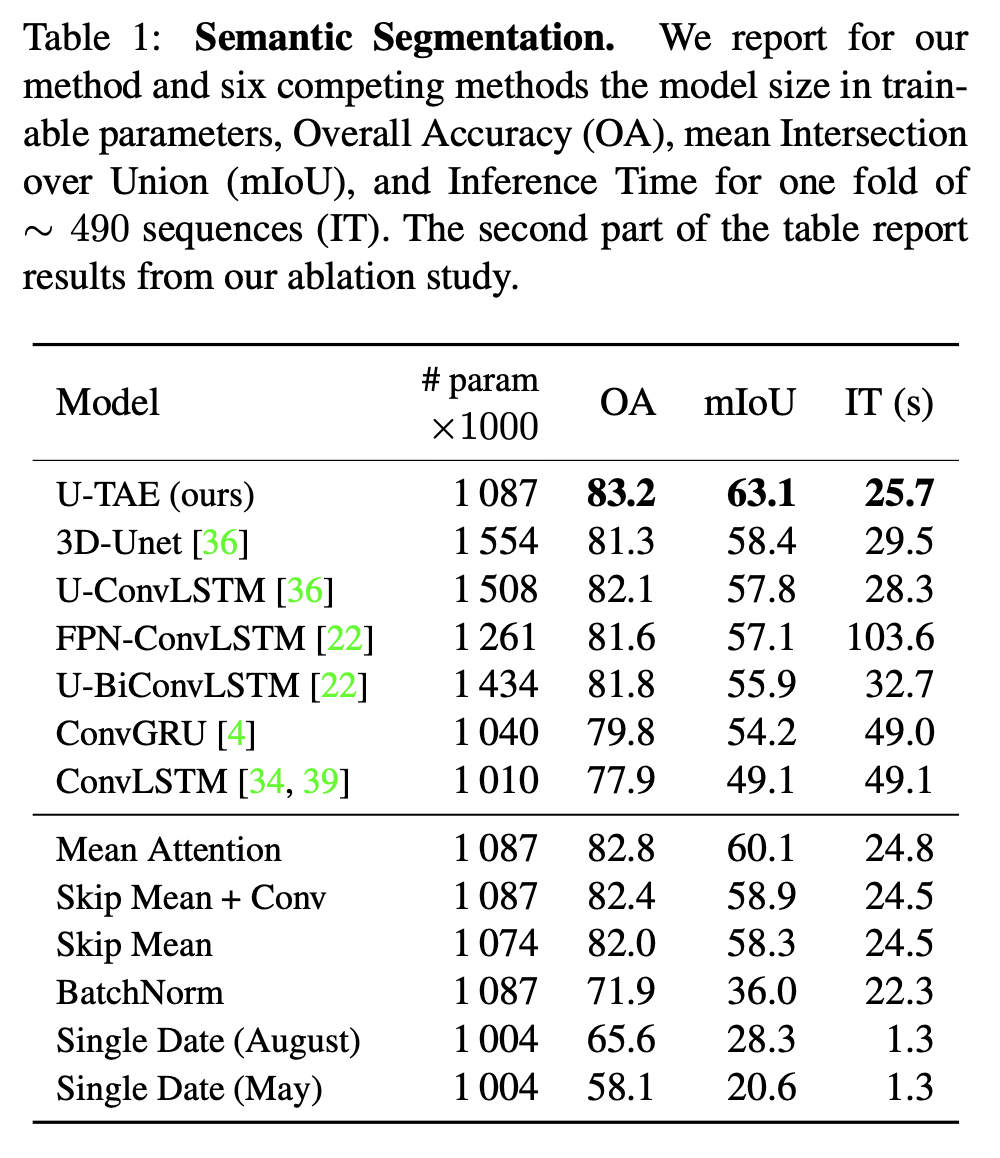
TSViT

1. 论文信息

属性	详细信息
标题	🔬 Vits for sits: Vision transformers for satellite image time series 🔬 适用于SITS的ViT：Transformer在卫星图像时间序列中的应用
会议	📚 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 🏆 CCF-A
日期	⏲️ 2023
作者	👨‍🔬 Michail Tarasiou

在 ViT 中，我们通常使用 Transformer-only 的主干网络来提取单幅图像的空间特征。当面对由多时相影像组成的 SITS 数据时，Transformer能否胜任呢？答案是可以的。

TSViT 正是将Transformer应用到 SITS 的一种方法。论文面向时空遥感序列提出了一种时空联合特征提取主干网络 | Backbone。该网络能从时序影像中为某一 patch 提取时间维度与周围空间的特征信息，并将该特征用于 pixel-wise 和 patch-wise 等下游预测任务。下面我们来逐步学习下 TSViT 的模型结构。

2. 模型结构

论文的 $\text{3. Method}$ 章节系统而清晰地介绍了 TSViT 的整体架构与若干关键设计细节，推荐阅读原文。为了更好地理解其核心思想，接下来我们将沿着作者的思路，一步步拆解模型的各个组成模块，看看 TSViT 是如何在时空两个维度上同时建模，并最终实现对 SITS 数据的高效表征。

🔍 多查询设计

在原始 ViT 中，通常在 patch token 序列前加入一个可学习的 cls token（即[CLS]），并将该 token 的最终状态作为整张图像的全局表示用于分类（即单一查询向量用于聚合全局信息）。这是 ViT 的标准做法并被大量后续工作采用。

TSViT 对这一点作了工程化与任务导向的扩展：引入 $K$ 个可学习的 cls token（此处 $K$ 与类别数相等），将这些 cls token 与 patch token 一起输入编码器，最后把每个 cls token 投影为一个标量并拼接得到长度为 $K$ 的 logits 向量。以下是论文原文的相关解释：

This design choice brings the following two benefits:

it in creases the capacity of the cls token relative to the patch tokens, allowing them to store more patterns to be used by the MSA operation; introducing multiple cls tokens can be seen as equivalent to increasing the dimension of a single cls token to an integer multiple of the patch token dimension $d_{cls} = k \cdot d_{patch}$ and split the cls token into k separate subspaces prior to the MSA operation. In this way we can increase the capacity of the cls tokens while avoiding is sues such as the need for asymmetric MSA weight matrices for cls and patch tokens, which would effectively more than double our model’s parameter count.

it allows for more controlled handling of the spatial interactions between classes. By choosing $k = K$ and enforcing a bijective map ping from cls tokens to class predictions, the state of each cls token becomes more focused to a specific class with net work depth. In TSViT we go a step further and explicitly separate cls tokens by class after processing with the temporal encoder to allow only same-cls-token interactions in the spatial encoder.

这种设计方案带来了以下两个方面的优势：

提升 cls token 的表达容量
相较于 patch token，cls token 拥有更大的存储空间，可捕捉和存储更多可供多头自注意力机制利用的模式。当引入多个 cls token 时，可以将其视为把单个 cls token 的维度扩展为 patch token 维度的整数倍，即 $d_{cls} = k \cdot d_{patch}$ 并在进入MSA之前将 cls token 拆分为 $k$ 个独立的子空间。这种方式不仅能够增强 cls token 的容量，还能避免设计不对称的MSA权重矩阵（分别作用于 cls 和 patch token），从而避免模型参数量增加至原先的两倍以上。

更可控的类别空间交互
通过设置 $k = K$ ，并在 cls token 与类别预测之间建立一一对应的映射关系，随着网络深度的增加，每个 cls token 的状态将逐渐专注于某一特定类别。在TSViT中，设计进一步扩展：在时间编码器处理完成后，显式地按类别区分 cls token，使得在空间编码器中仅允许相同类别的 cls token 进行交互。

TSViT 在时间编码器处理后还按类别显式分离 cls token，从而在空间编码器中仅允许「同类 cls token 」之间交互，这被作者视作对作物类型识别有益的 归纳偏置 | inductive bias 。

需要特别说明的是，TSViT 并未改变模型最终输出的形状：ViT 往往将单个 cls token 的 $d_\text{model}$ 映射到类别维度 $K$ （ $d_\text{model}\to K$ ）；而 TSViT 则对 $K$ 个 cls token 各自进行 $d_\text{model}\to 1$ 的投影，再拼接得到 $K$ 维输出——二者在输出维度上等价，但内部的表征与交互方式不同（即内部并行化为类专属通道）。整个过程如下图所示：

figure 2.2. 主干网络设计

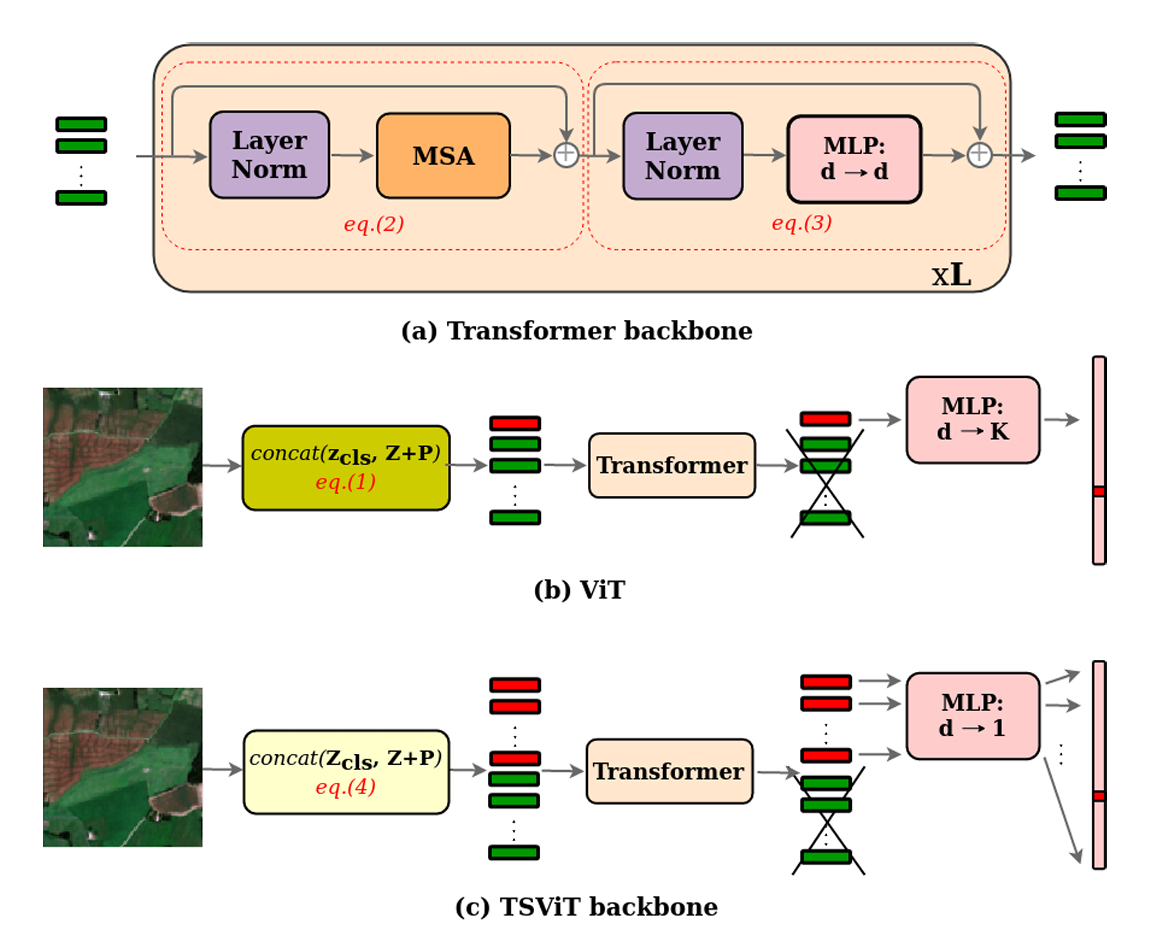
在作者的消融实验（Germany 数据集）中，将分解 | factorization 顺序改为 temporo-spatial 后，mIoU从 $48.8\%$ 跳升至 $78.5\%$ ；在此基础上加入额外的 cls tokens（即多查询设计）可把mIoU从 $78.5\%$ 提升到 $83.6\%$ ，因此作者在最终模型中采用了 $K$ 个 cls tokens。论文同时还说明了对 cls token 映射后再拼接的必要性：若允许不同 cls token 在空间编码器中任意交互，则会带来性能下降（ $−2.1\%$ mIoU），且计算代价显著增加。

最后说一下我的理解，论文中的消融实验显然证明了 cls token 与分类类别一一对应这一设计的有效性，但该设计在此前的研究中显然也有应用，TSViT 模型的重点还是在接下来介绍的几个章节中。

🫎 编码器架构

在介绍TSViT的时空编码器模块之前，我们不妨先回顾一下 ViT 是如何使Transformer能够处理图像的。ViT 的核心思想是将输入图像划分为若干个固定大小的二维patch，并将每个patch内的像素展平为一维向量，作为Transformer的输入token。为了让Transformer感知这些 patch token 在空间上的相对位置信息，ViT 还需要在特定阶段引入 位置编码。这一处理步骤使得原本针对一维序列设计的Transformer可以自然扩展到二维图像建模任务中。

基于这一思路，若我们从构建 TSViT 的角度出发，面对的是比单幅影像更复杂的 时序遥感影像 数据。与 ViT 输入的二维图像不同，SITS在空间 $(H, W)$ 之外还多了一个时间维度 $T$ 。为了同时建模时空信息，可以借鉴视频理解领域的研究思路——即在空间patch划分的基础上，将划分方式扩展到时间维度。具体来说，给定输入数据 $X \in \mathbb{R}^{T \times H \times W \times C}$ ，在时间与空间维度上应用一个大小为 $(t \times h \times w)$ 、步长为 $(t, h, w)$ 的三维卷积核，从而把原始数据划分为一系列时空patch。最终得到的序列长度为：

\begin{align*} N = \left \lfloor \frac{T}{t} \right \rfloor\cdot\left \lfloor \frac{H}{h} \right \rfloor \cdot \left \lfloor \frac{W}{w} \right \rfloor \end{align*}

其中每个 token 同时包含了局部的时序与空间信息，其尺寸为 $\mathbb{R}^{thwC}$ ，然后我们再将 patch token 投影到 $d_\text{model}$ 维度，最终得到了适用于Transformer的输入序列。

据论文中描述，经过实验验证这里的 $t$ 的最佳参数设置是 $t=1$ ， $h$ 、 $w$ 的最佳取值则参考消融实验结果（同样也是越小越好 $2\times 2$ ）。

对于 $t=1$ 我的理解是，通过这样设置，我们在使用线性映射初步提取patch内信息时将着重于空间尺度，对于时间尺度的信息提取则主要是在后续的Transformer编码器中实现。换句话说， $t=1$ 的设置避免了在patch划分阶段直接把时间信息与空间信息 混合压缩 ，从而保留了更细粒度的时间分辨率。这种做法不仅使得模型能够更灵活地在后续模块中建模时序依赖关系，同时也避免了过早的时间维度下采样带来的信息损失。

面对这样的输入序列，我们当然可以将其进行位置编码后直接送入Transformer编码器中处理，但这有两个问题：

计算复杂度过高：自注意力机制的计算成本与序列长度呈 $\mathcal{O}(N^2)$ 的关系。当我们为了提高时空分辨率而采用较小的patch尺寸划分 SITS 数据时，序列长度 $N$ 会急剧增长，导致注意力计算的代价呈平方级膨胀，在实际应用中几乎不可接受。
时空建模不均衡：如果在位置编码设计上未能妥善区分并平衡时间与空间两个维度的作用，Transformer可能会难以从长序列中有效捕捉时间依赖关系，从而无法充分建模SITS数据的时序特征。

为了避免这些问题，TSViT 选择将输入序列按时间和空间维度分解，通过分别处理SITS数据的时间特征和空间特征，从而缩短Transformer实际处理的序列长度。TSViT 的时空编码器结构如下图所示：

figure 2.4. TSViT子模块（1）

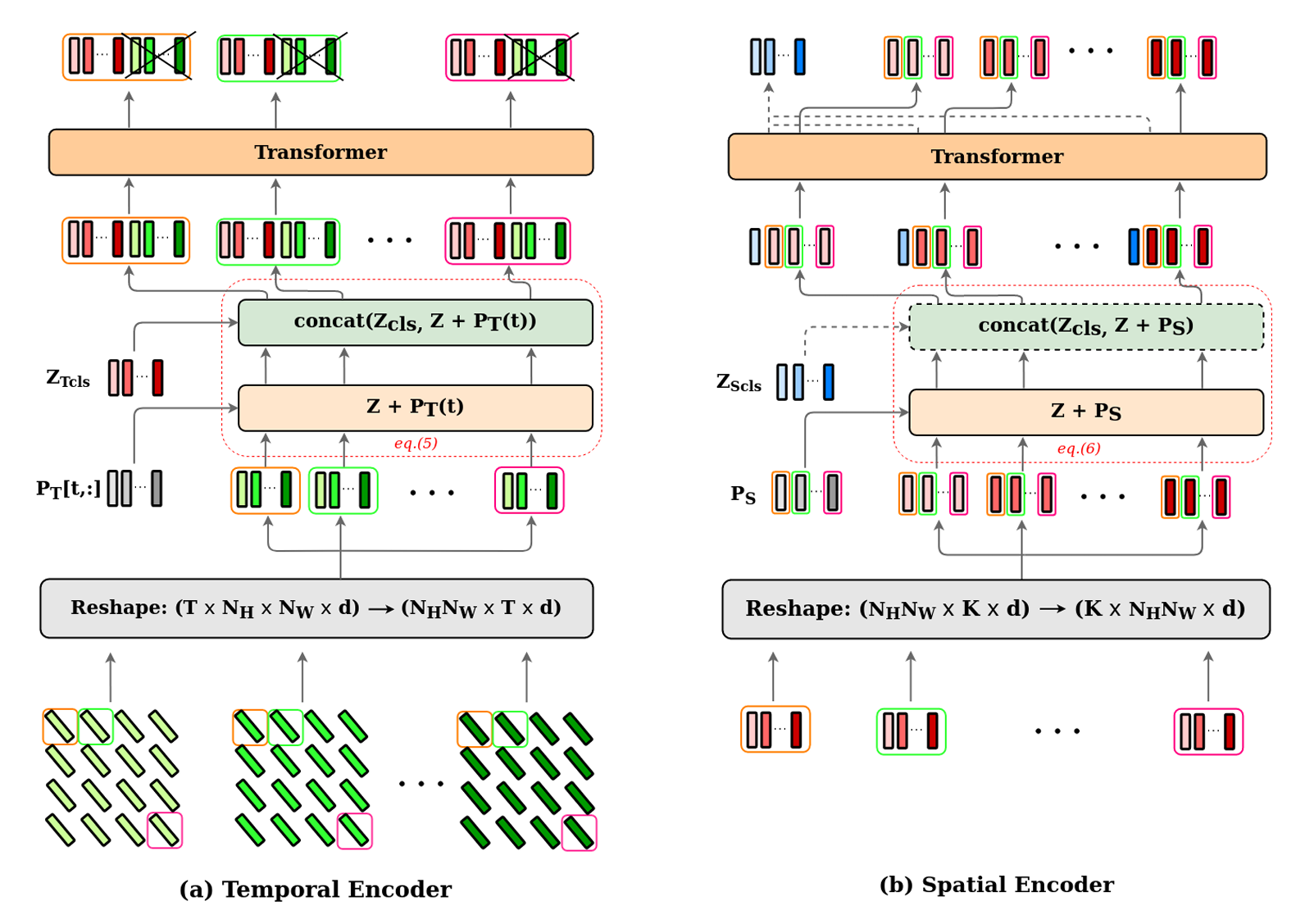
这里简单说明一下我对 TSViT 编码器的理解，TSViT 对输入序列的时序分解实际上是将同一个patch划分在不同时间点上的 patch token 重组为一个新的时间序列，然后我们便可以利用 Transformer 捕捉其随时间演化的特征。从论文中的示意图也能看出，该阶段所用的位置编码并非固定模式，而是根据每幅影像的实际观测时间生成，位置编码的具体实现细节这里就不过多讲解。

我们假设一个SITS数据序列化后得到大小为 $(N_T\times N_H\times N_W\times d)$ 的 patch token 集合，其中 $N_T$ 表示时间步数， $N_H \times N_W$ 表示空间划分的 patch 数量， $d$ 是 token 维度。时序分解将序列重塑为 $\text{Z}_{\text{T}} \in \mathbb{R}^{N_HN_W\times N_T\times d}$ ，则时间编码器的输入为：

\begin{align*} \mathbf{Z}_\text{T}^0 = \operatorname{concat}(\mathbf{Z}_\text{Tcls}, \mathbf{Z}_\text{T} + \mathbf{P}_\text{T}[t,:]) \in \mathbb{R}^{N_HN_W\times (K+N_T)\times d} \end{align*}

其中， $\mathbf{Z}_\text{Tcls} \in \mathbb{R}^{K \times d}$ 表示 $K$ 个类别相关的查询向量； $\mathbf{P}_\text{T}[t,:] \in \mathbb{R}^{N_T \times d}$ 为基于观测时间生成的时间位置编码；拼接操作使得每个时序序列长度扩展为 $K + N_T$ ，即除了 $N_T$ 个 patch token 外，还额外包含 $K$ 个查询 token。需要注意的是，在Transformer内部，实际处理的是长度为 $(K + N_T)$ 、维度为 $d$ 的一维序列。而在具体实现中，通常会将 $(N_H N_W)$ 这一维度与 batch size 合并，以便批量计算并提升效率。最终我们选取时间编码器的前 $K$ 个 cls token 作为当前patch划分的时序特征输出，其中每一个 cls token 可以被视作该patch针对某一类别的提取的二分类判别特征。

由图可知，TSViT 的空间编码器结构在整体上与 ViT 类似，可以理解为：利用一个共享的Transformer编码器，对 $K$ 个类别相关的二维特征图分别进行空间特征提取，从而为下游分类或分割任务提供判别性特征。在进入空间编码器之前，需要将时间编码器输出的张量按照空间维度重新排列，以确保序列与原始SITS数据的空间分布保持一致。空间编码器的输入为：

\begin{align*} \mathbf{Z}_\text{S}^0 = \operatorname{concat}(\mathbf{Z}_\text{Scls}, \mathbf{Z}_\text{S} + \mathbf{P}_\text{S}) \in \mathbb{R}^{K\times (1+N_HN_W)\times d} \end{align*}

需要注意的是，在 ViT 中通常只引入一个 cls token，用于在Transformer的训练过程中聚合整个序列的信息；而在 TSViT 的空间编码器中，虽然整体结构依然源自 ViT，但其建模目标可以被理解为对 $K$ 个类别相关的特征图独立进行空间特征提取。因此，聚合空间信息的 cls token 也应当扩展为 $K$ 个，对应于 $\mathbf{Z}_\text{Scls} \in \mathbb{R}^{K\times 1\times d}$ （ $K$ 个 cls token 与分类类别存在一一对应关系，不同类别的特征图序列应当与对应 cls token 构成长为 $1+N_HN_W$ 的新序列）。经过空间编码器的处理后，输出序列可自然分为两部分：

cls token（ $1 \times d$ ）：为当前特征图对于类别的全局表征；
patch token（ $N_HN_W\times d$ ）：各patch内的局部表征；

通过将这两类 token 拆分并重组，TSViT 最终能够同时输出适用于 patch-wise 与 pixel-wise 的时空特征。这一设计不仅满足了分类任务对全局语义的需求，同时也为语义分割等 密集预测 任务提供了充分的空间上下文。

通过上述讲解我们大致了解了 TSViT 编码器的结构，下面还补充一下针对 TSViT 编码器中各个序列的可视化说明：

时空编码器中的尺寸可视化

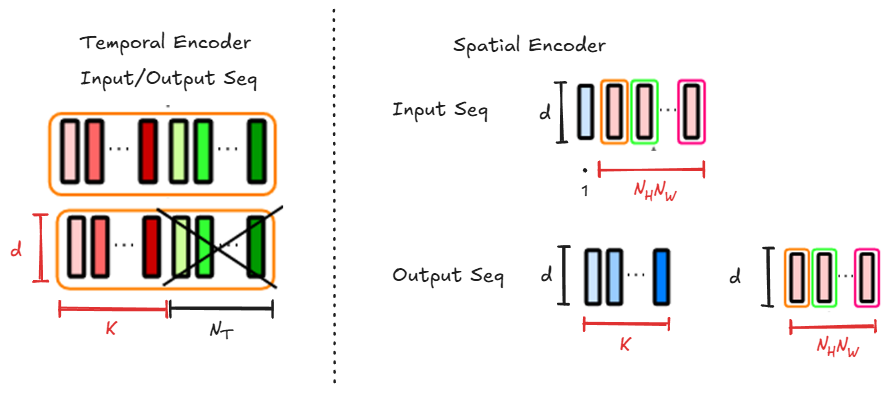
🦄 解码器架构

由于 TSViT 编码器能够同时提取适用于全局任务和密集预测任务的时空特征，作者在设计时为两类任务分别配置了相应的 解码器头部 。具体来说，TSViT 的解码器主要由MLP层以及若干矩阵运算组成，其整体结构如下所示：

figure 2.4. TSViT子模块（2）

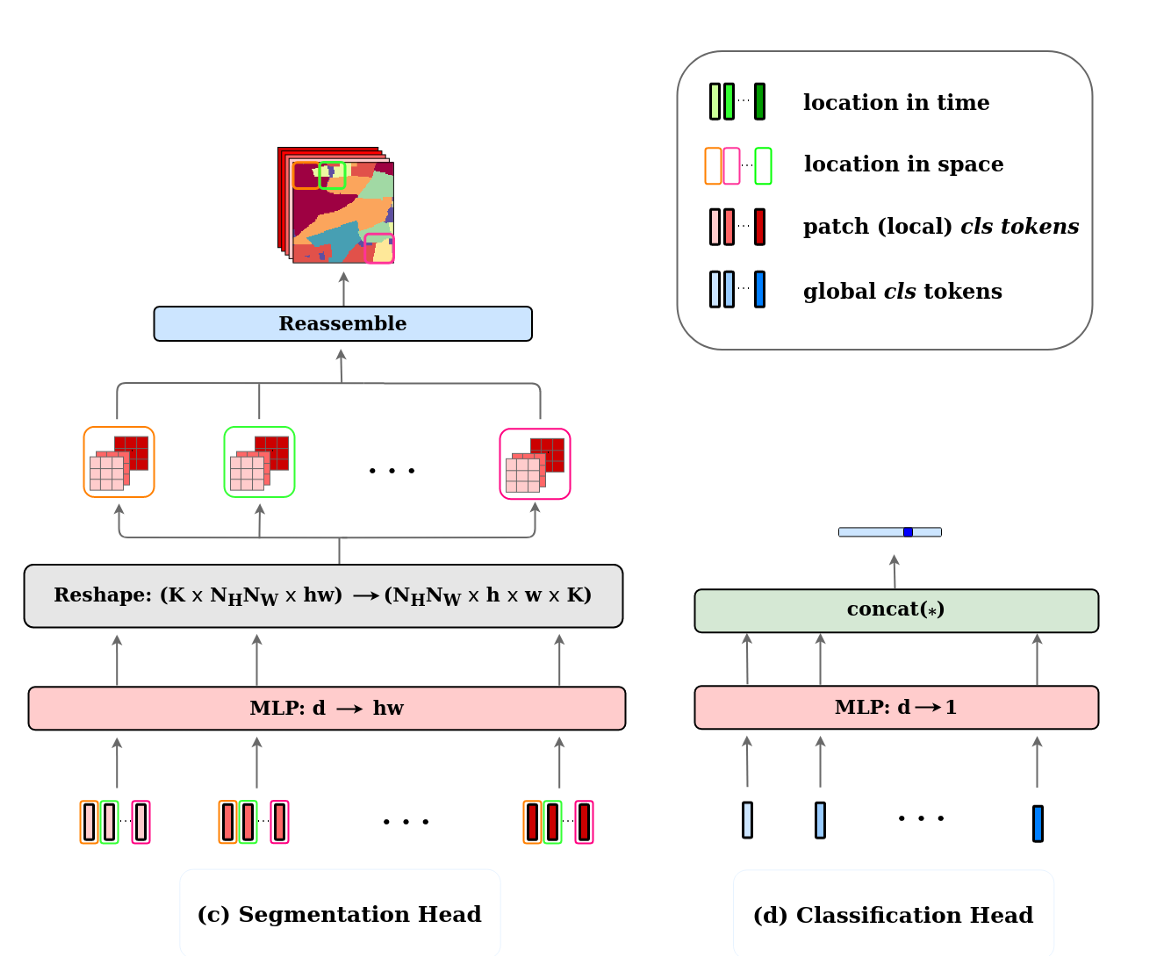
从图中可以看到，空间编码模块会为每个patch提取出一个对应某一类别（ $K$ 个类别）判别特征向量，该向量的维度为 $d$ ，其中蕴含了该patch内所有像素的分类判别信息。通过MLP层，这些判别信息能够进一步映射到像素级别，从而实现语义分割任务，这正是图中 $(c)$ 分割头的作用。

另一方面，在空间编码过程中引入的[CLS] token 用于聚合全局空间分布信息。该全局判别向量同样具有维度 $d$ ，可以通过映射转换为整体 parcel 的类别预测，从而满足图像级别的分类任务需求。

UTS-Former

1. 论文信息

属性	详细信息
标题	🔬 A temporal-spatial deep learning network for winter wheat mapping using time-series Sentinel-2 imagery 🔬 基于时间序列Sentinel-2遥感影像的冬小麦空间-时间深度学习网络
期刊	📚 ISPRS Journal of Photogrammetry and Remote Sensing 🌍 地球科学1区 [TOP]
日期	⏲️ 2024
作者	👩‍🔬 Lingling Fan

UTS-Former 可以视作 UTAE 的改进版本。其核心思想在于，用 全局自适应池化 | GAP 与改进后的 TSViT 替代 UTAE 中对时间维度 $T$ 的降维操作（L-TAE 注意力机制），从而使解码器部分更自然地迁移到 UNet 范式下。

需要说明的是，原论文的研究任务是针对冬小麦的 SITS 数据进行二分类语义分割，这与我的研究内容有些区别，因此这里仅聚焦于论文的「实验数据」与「模型构成」这两个主要内容。

2. 模型结构

UTS-Former 模型结构如下所示：

figure 3.3. UTS-Former整体架构图

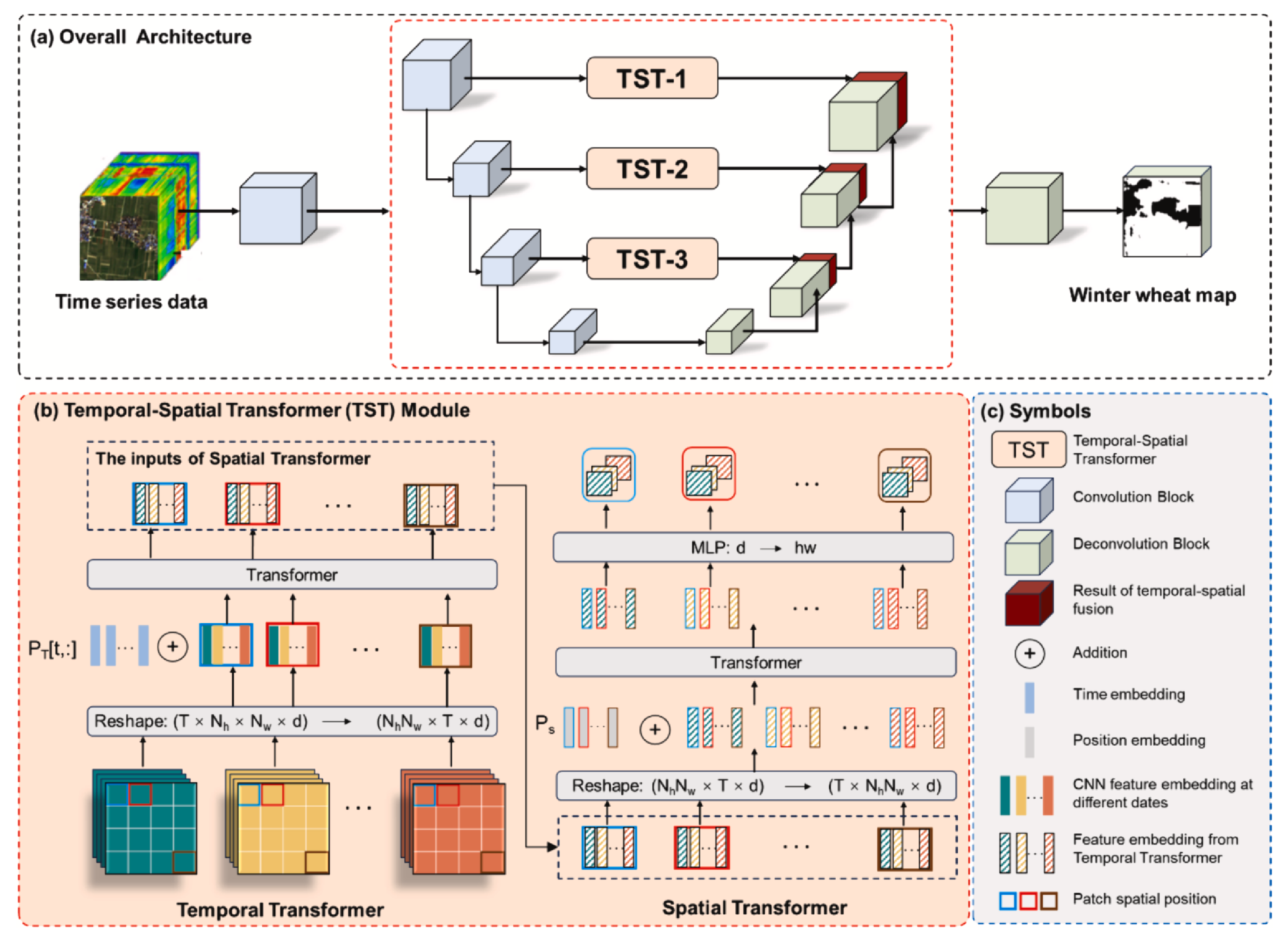
🤖 编码器设计

由于该论文并未公开模型源码，我们无法直接通过代码解析其结构。因此，这里主要基于论文原文的描述，结合个人理解，对模型结构的细节进行梳理与说明。接下来将从 编码器 部分入手，逐步介绍 UTS-Former 的整体设计。

与常见的基于 SITS 数据的时序遥感影像分割任务类似，UTS-Former 在每一层编码器中的输入数据均组织为形状 $T \times H_l \times W_l \times C_l$ 的张量（此处暂不考虑批次维度）。在接收到该张量后，模型首先采用与 UTAE 相近的策略：对每个时间步的影像分别进行二维卷积运算，以完成该时刻影像的空间特征编码。为保证准确理解，我们不妨结合原文解读其结构。

We input the temporal sequence images into the encoder network with a stride of 2, kernel size of $3\times 3$ , spatial resolution of $256\times 256$ and maximum length of the time series of 32. During the training process, we used masks to supplement the missing sequences if the temporal sequence number was less than 32. However, flexible input based on the actual sequence length was allowed during the testing process. The input channels include 9 spectral bands and 1 temporal channel, while the temporal channel is used only in the TST modules. The temporal channel refers to the actual acquisition dates of the images, and is designed to introduce temporal sequence information to the TST module. To obtain the temporal channel, we converted the acquisition date of each image to the day of the year (DOY) and extended it into a matrix with the same spatial resolution as the image to match the resolution of the input image. Considering the high computational complexity of 3D CNNs, the convolutional layers of the encoder are implemented using 2D CNNs, and the time dimension “T” is merged into the batch dimension. We obtained feature maps of scales 128, 64, 32, 16, and 8 after 5 CNN layers. Each CNN layer comprises a $3\times 3$ convolution operation, a batch normalization operation, and a rectified linear unit (ReLU) activation layer. To reduce spatial information loss, we employed convolutional layers with a stride of 2 instead of pooling operations for downsampling.

我们将时间序列图像输入编码器网络，步长为2，卷积核尺寸为 $3\times 3$ ，空间分辨率为 $256\times 256$ ，时间序列最大长度为32。训练过程中，若时间序列数量少于32，则使用掩码补充缺失序列。但在测试阶段允许根据实际序列长度进行灵活输入。输入通道包含9个光谱波段和1个时间通道，其中时间通道仅用于TST模块。该时间通道记录图像的实际采集日期，旨在为TST模块引入时间序列信息。为获取时间通道，我们将每幅图像的采集日期转换为年度天数（DOY），并扩展为与图像空间分辨率相同的矩阵以匹配输入图像。鉴于三维卷积神经网络（3D CNN）的高计算复杂度，编码器的卷积层采用二维卷积神经网络实现，并将时间维度“T”合并至批量维度。经过5层卷积网络处理后，我们获得了128、64、32、16和8个尺度的特征图。每层卷积网络包含 $3\times 3$ 卷积操作、批量归一化操作及ReLU激活层。为减少空间信息损失，我们采用步长为2的卷积层替代池化操作进行降采样。

🔹 时间通道

所谓时间通道，实际上是指各时间刻影像中每个像素对应的 DOY（Day of Year）信息。在 UTS-Former 中，该通道仅用于 TST 模块的位置编码。之所以被视为编码器的输入，是因为在送入 TST 之前，需要先将每幅图像的 DOY 值扩展到与各编码器处理尺度相匹配的空间分辨率。这可被视为 TST 的预处理环节，作者因此将其归类为编码器输入的一部分。

🔹 二维卷积层

通常，在 SITS 数据的空间特征提取中，会针对单一时间刻影像独立进行卷积编码。但通过对 TSViT 的分析不难发现，也可以将相邻时间刻的影像组合在一起进行空间编码，从而不仅获得空间特征，还能在一定程度上捕获短时间范围内的动态变化。

在具体实现上，TSViT 将该时空张量通过Conv3D（在实现效果上等价于FC层）映射为维度 $d_\text{model}$ 的一维向量，再送入Transformer处理。而类 UTAE 的模型同样可以采用这种方式。不过根据 TSViT 的实验结论，时间刻的最优分割尺度为 $t=1$ ，因此 UTS-Former 也遵循这一设置。在该条件下，Conv3D 的运算可以直接使用Conv2D实现。

🤔 一些思考

当我们使用 $t>1$ 的尺度分割 SITS 数据的时间维度时，空间编码模块输出的时序长度将会发生变化，从而对 TST 模块中的时间位置编码提出新的挑战。这一点可能正是潜在的改进方向。

一种可能的思路是：在输出某一时间刻特征图时，同时利用其前后时间刻的影像数据，以获得更加稳定的时序表征。至于特征提取方式，可以选择传统卷积，也可以直接采用论文提出的 TST 模块。

🔹 下采样

采用可训练的卷积层代替不可训练的池化层实现下采样。

🐎 TST模块

UTS-Former 在类 UTAE 的结构中引入了 时空Transformer | TST ，以实现降维跳跃连接。该模块的设计结构如下图所示：

figure 3.4. TST模块结构（a）时间Transformer（b）空间Transformer

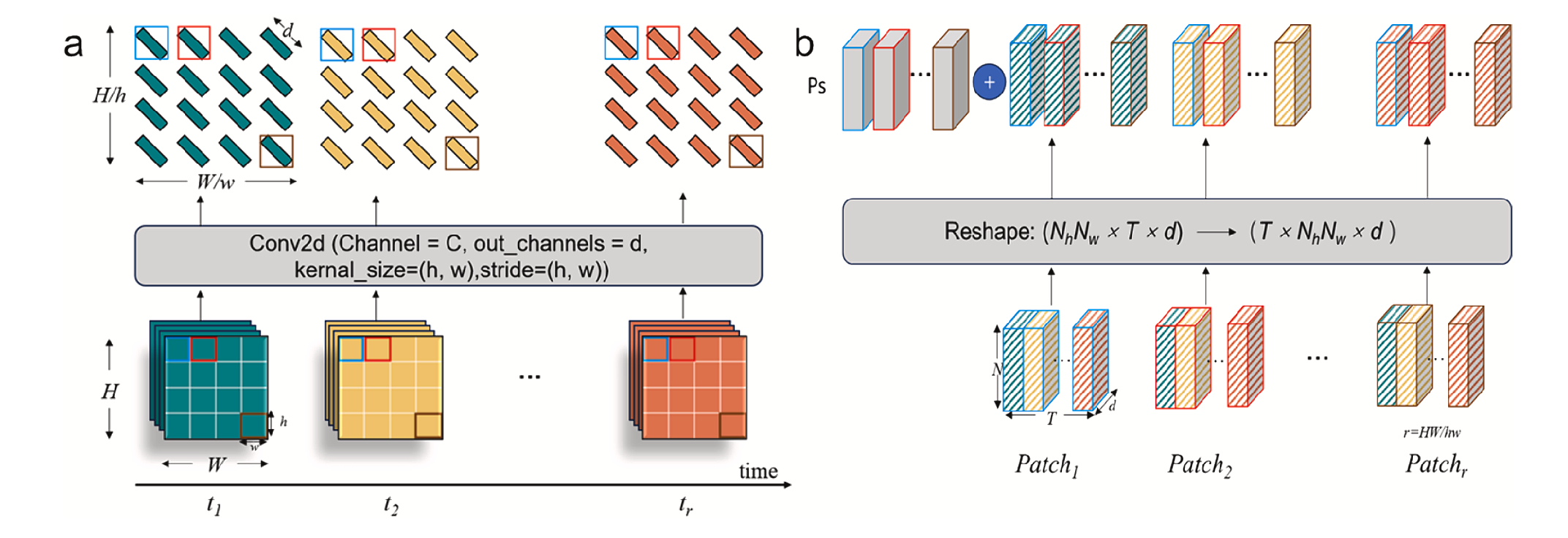
在介绍其具体结构之前，我们不妨先回忆一下 TSViT 的主干网络结构：TSViT 通过在时间编码模块中引入与分类类别一一对应的查询向量（[CLS] token），从而实现了对每个 patch 时序数据的类别特征提取。

然而，如果在时间编码中不引入查询向量，会发生什么呢？这种情况下，时间编码模块将仅为时序序列中的每个元素添加全局上下文信息，而不会显式生成类别相关的表示。TST 模块正是采用了这种设计：其时间编码模块的输入与输出数据维度保持一致：

\begin{align*} \mathbf{X}^{\text{T}}_{\text{in}},\mathbf{X}^{\text{T}}_{\text{out}}\in \mathbb{R}^{N_hN_w \times T \times d} \end{align*}

随后，TST 将时间编码模块的输出重新组织为：

\begin{align*} \mathbf{X}^\text{S}_\text{in} \in \mathbb{R}^{T \times N_hN_w \times d} \end{align*}

并将其送入空间编码模块。该模块由 Transformer 与 MLP 共同构成，能够在空间维度上进行特征交互与聚合。最终，模型完成了时序全局特征与空间特征的联合编码，实现了通道信息的有效融合，其输出维度变化如下：

\begin{align*} (T \times H_l \times W_l \times C_l) \to (T \times H_l \times W_l) \end{align*}

🤯 跳跃连接与解码器设计

由 UTS-Former 架构图可知，在U型结构的最底层“连接”中，模型并未引入 TST 模块降低编码器输出张量的维度。根据原论文描述，UTS-Former 采用 全局自适应池化 | global adaptive pooling 实现信息降维。

In the decoder, the global adaptive pooling operation is first applied to the temporal dimension T, enabling channel fusion with the output of TST. The decoder employs 2D convolutions and generates feature maps with scales of 8, 16, 32, 64, and 128 after 5 deconvolution layers. Each deconvolution layer consists of a $3\times 3$ convolution layer, a batch normalization layer, a ReLU activation layer, and a deconvolution layer with a stride of 2. The local information extracted by the CNN is fused with the global information extracted by the TST at scales 16, 32, and 64, effectively modeling both temporal and spatial features. Finally, we used a deconvolution operation in the segmentation head, where the output channels were set equal to the number of classification types, to achieve the final winter wheat classification.

在解码器中，首先对时间维度T应用全局自适应池化 （GAP）操作，实现与TST输出通道的融合。解码器采用二维卷积，经过5层反卷积后生成8、16、32、64和128个尺度的特征图。每个反卷积层包含： $3\times 3$ 卷积层、批量归一化层、ReLU激活层及步长为2的反卷积层。在16、32、64尺度上，CNN提取的局部信息与TST提取的全局信息实现融合，有效建模时序与空间特征。最终在分割头部采用反卷积操作，其输出通道数设置为分类类型数量，从而实现冬小麦的最终分类。

原文对解码器的描述更偏向整体视角。其中提到的 全局自适应池化 操作，其实仅作用于最底层编码器的输出特征。结合后文“实现与 TST 输出通道的融合”的描述，可以推测该操作的作用是：在空间尺度上对齐处理后的特征张量与 TST 模块的输出，使二者能够在不同层次间逐一对应。因此，这里的尺度变化可能是：
$\begin{align*}(T \times H_L \times W_L \times C_L^\text{enc}) \to (H_L \times W_L \times C_L^\text{dec})\end{align*}$
GPT给出的解释是，这里针对时间维度的池化操作将时间维度由 $T$ 压缩到 $1$ ，实现了时间维度的降维，若没有其他操作，则 $C_L^\text{enc} = C_L^\text{dec}$ 。那么「全局自适应池化 」这一描述就存在问题（这里并没有体现自适应的特点），可能的解释有：

GPT 的解释是：池化操作主要针对时间维度，将其由 $T$ 压缩至 $1$ ，实现时间维度的降维。如果不考虑额外的通道变换，那么 $C_L^\text{enc} = C_L^\text{dec}$ 。由此可见，论文中将该操作称为「全局自适应池化」可能存在一定歧义，因为其“自适应”的特性并未在文中充分体现。更合理的解释有两种可能：

针对时间序列长度的自适应：由于 SITS 数据的时间维度 $T$ 在不同任务中并不固定，模型需要能够在该位置动态调整池化尺度，从而对不同长度的输入序列保持适应性。

理解偏差的可能性：也可能是我对论文相关表述的理解存在不足。

我们可以将 GAP 提取的特征理解为每个通道上的 时序聚合特征（即时间维度被消除后得到的通道表征）；而跳跃连接的特征则可以看作每个时间刻的 通道聚合特征（即通道维度被消除后得到的时间表征）。在这种设计下，二者拼接后的特征张量维度为：

\begin{align*} \mathbf{X}_l^\text{skip} \in \mathbb{R}^{H_l \times W_l \times (C_l^\text{dec} + T)} \end{align*}

总体来说，每个解码器单元可以解释为：使用 通道聚合特征 恢复对应尺度的 时序聚合特征（PS：这个解释是在太过牵强，有“拼积木”的嫌疑）。在将时序特征图转换成了形如 $H_l \times W_l \times (C_l^\text{dec} + T)$ 的三维特征图后，我们便可自然而然地将其用于 UNet 解码器的范式中，其实现细节参考上述论文描述。

3. 实验数据

UTS-Former 所使用的实验数据如下表所示：

要点	说明
影像	Sentinel-2影像，RGB、R1/2/3（红边）、NR（近红外）、SW1/2（短波红外）
分布	8个站点（6个作为训练样本，2个作为测试集），每个站点覆盖约为 $5000\times 5000$ 像素由于每个站点覆盖范围面积类似，训练样本数与测试集数也应该大致为 $6:2$ ；
样本	3年制图产品（2020-2022）作为训练数据，根据 `patch_size=256`、`stride=128` 生成 $38,000^?$ 个训练样本（训练集:验证集 = $8:2$ ）这里的 $38,000$ 是正确的数值，一个站点最多可分 $\left\lfloor (5000+128)/128\right\rfloor^2$ 个样本块，8个站点3年可生成 $40^2\times 8 \times 3 = 38400$ 个样本块（该样本数不具备参考性）。