本文内容来源于网络博客及GPT生成内容,作者并未详细阅读论文原文
FCN
1. 论文信息
| 属性 | 详细信息 |
|---|---|
| 标题 | 🔬 Fully Convolutional Networks for Semantic Segmentation 🔬 全卷积神经网络在语义分割中的应用 |
| 会议 | 📚 Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 🏆 CCF-A |
| 日期 | ⏲️ 2015-06 |
| 作者 | 👨🔬 Jonathan Long |
2. 模型结构
FCN是一种用于图像语义分割的网络,是深度学习用于语义分割领域的开山之作。

图1是FCN论文中的原图,其中提到了 密集预测 | dense-predict ,这一术语是指网络对输入图像的每一个位置(通常是像素)都做出预测,而不是对整个图像输出一个或多个值。我的理解是:密集预测任务是 patch2patch 形式的任务,如果用CNN实现输入一个patch输出一个值,然后再滑动输入窗口实现语义分割这种任务则不是密集预测任务。
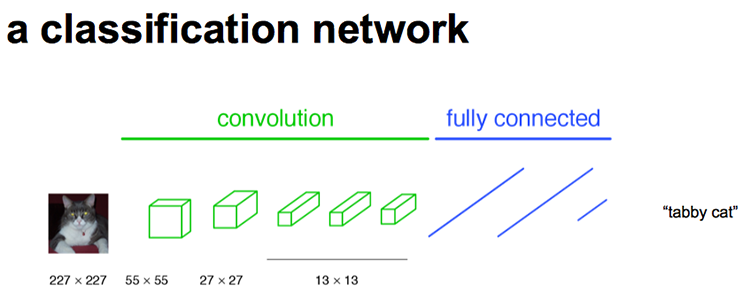
flatten为一维向量投入FC中事实上,这类通过滑动实现的分割方式可以被称为 滑窗预测 | sliding window (或patch-wise prediction)。需要注意的是,遥感语义分割的结果往往需要拼接输出最终分类大图,但模型在处理每个patch时实际上还是做的dense-predict,因此不算patch-wise predict。
卷积层(Conv)和全连接层(FC)都是在做 点积运算 | dot product ,只是卷积层有局部连接和参数共享的特性。因此,在某些情况下两种是可以相互转换的。例如,一个输入为7x7x512,输出为4096的全连接层(输入为卷积层输出的flatten结果)可以由kernel_size=7、kernel_number=4096、stride=1、padding=0的卷积层代替,最终输出的是一个1x1x4096的特征图。当前,输入输出都是一维向量的全连接层也可以转换为1x1 Conv2D实现。
🔹 连接 |
Connection在神经网络中,连接描述的是输入层与输出层神经元(一般为像素)之间的计算关系。
🔹 全连接 |
Fully Connected在全连接层中,每个输出神经元都与所有输入神经元相连接,形成一个完全连接的图结构。若输入层大小为 ,输出层大小为 ,那么该层参数总数为:;
这使得全连接层表达能力强,但参数量大,易过拟合,尤其在处理图像时缺乏空间结构建模能力。
🔹 局部连接 |
Local Connectivity与参数共享卷积层则采用局部连接机制,每个输出神经元仅与输入中的一小块区域相关,这部分与卷积核大小相同的输入层区域被层为 感受野 |
receptive field。如果将卷积层的输入输出层摊平为类全连接层表示,则每个输出层神经元在计算时都共享了参数。若输入特征图的通道数为 ,尺寸为 ,输出特征图的通道数为 ,卷积核的大小为 (
Conv2D卷积核深度一般等于输入图通道数),则该卷积层的参数总数为:,该层最终使用了 个卷积核,最后的 表示偏置项参数数。
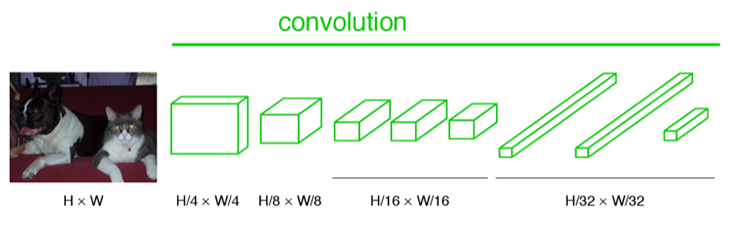
经过上述变化,传统CNN可被改造为由纯卷积层构成的全卷积网络FCN*。为了保留空间信息,FCN*最后三层卷积的输出被调整为尺寸为 的特征图,通常称为heatmap。这一部分可以被视为FCN的encoder,其输出通道数一般设为分割类别数 (也可为 ,再在decoder中映射到 )。因此,FCN*输出特征图的尺寸为 (对应FCN-32s/16s/8s)。
◀️ 反卷积
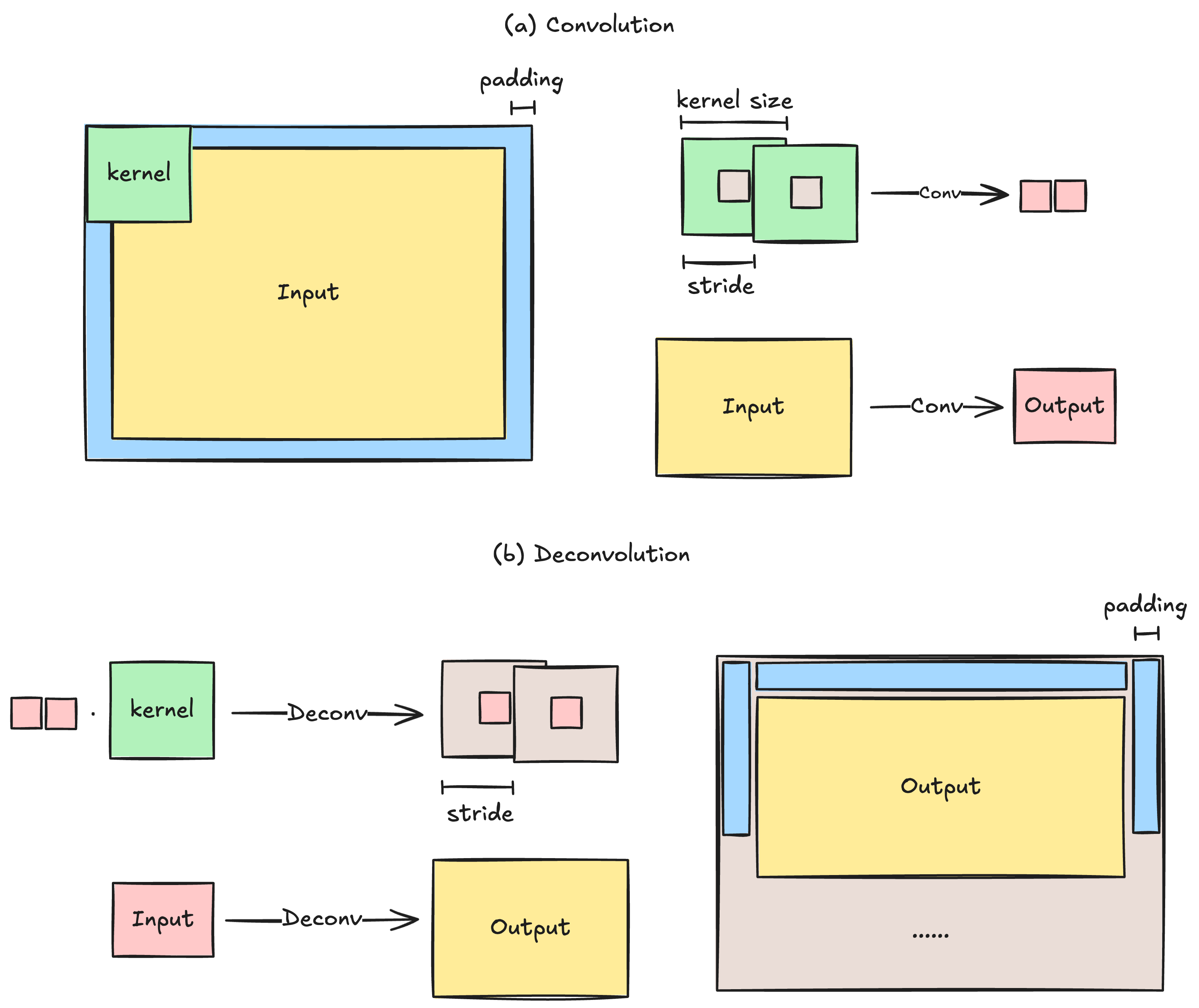
我们得到了可以表示各区域像素分割的热图后还需要还原成原图大小,这时候就需要引入一种可训练的上采样方法——反卷积(转置卷积),反卷积相较于普通卷积需要注意:
- 普通卷积的
padding用于填充输入以保证卷积核以整数步数滑动,而反卷积则是在输出特征图后根据设置padding进行裁剪。 - 由普通卷积示意图可知,
stride是两个相邻感受野中心点的间隔数+1,因此反卷积也可以设置stride控制输出特征图的 “感受野” 间隔(重叠部分相加)。 - 反卷积操作输出的特征图通道数与反卷积核 深度 |
depth有关。当输入特征图有多个通道时,最后的结果是对每个通道单独计算再将结果累加而成。
假设输入特征图尺寸为 ,核大小为 ,步幅为 ,填充为(可选),则反卷积操作的输出尺寸 为:
💃 跳跃连接
我们使用FCN的decoder结构,将特征图还原到原图大小。如果 解码器 仅在 编码器 最后层输出的特征图上进行上采样,最终的分割效果往往并不理想。因为最后一层的特征图太小,这意味着过多细节的丢失。因此,我们可以引入跳跃连接将最后一层的预测(全局信息)和更浅层(局部信息)的预测结合起来,在遵守全局预测的同时进行局部预测。
FCN中通常是使用各个池化层的输出作为浅层信息输入,而连接则是通过特征值相加实现,这样能保证解码器中各特征图的通道数始终与类别数一致。经典FCN结构如下:
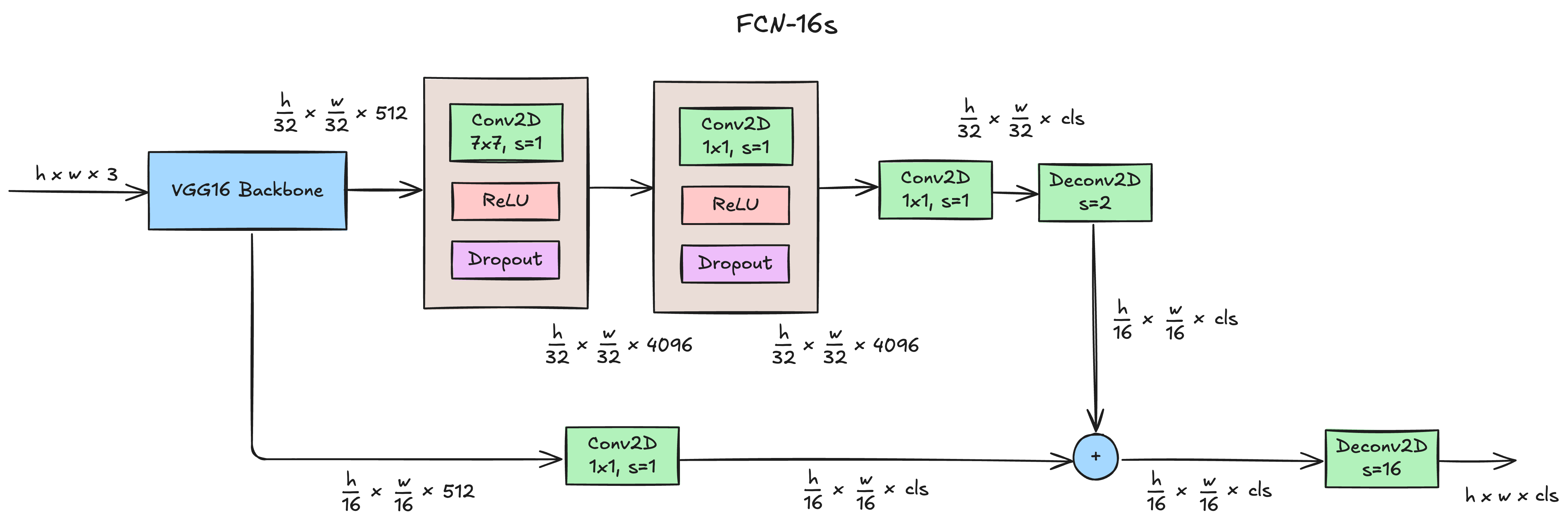
stride,同时也是反卷积放大倍数UNet
1. 论文信息
| 属性 | 详细信息 |
|---|---|
| 标题 | 🔬 U-Net: Convolutional Networks for Biomedical Image Segmentation 🔬 U-Net:用于生物医学图像分割的卷积神经网络 |
| 会议 | 📚 International Conference On Medical Image Computing And Computer-assisted Intervention (MICCAI) 🏆 CCF-B | 医学 |
| 日期 | ⏲️ 2015-11 |
| 作者 | 👨🔬 Olaf Ronneberger |
2. 模型结构
UNet是一种为医学图像分割而设计的神经网络,其结构如下:
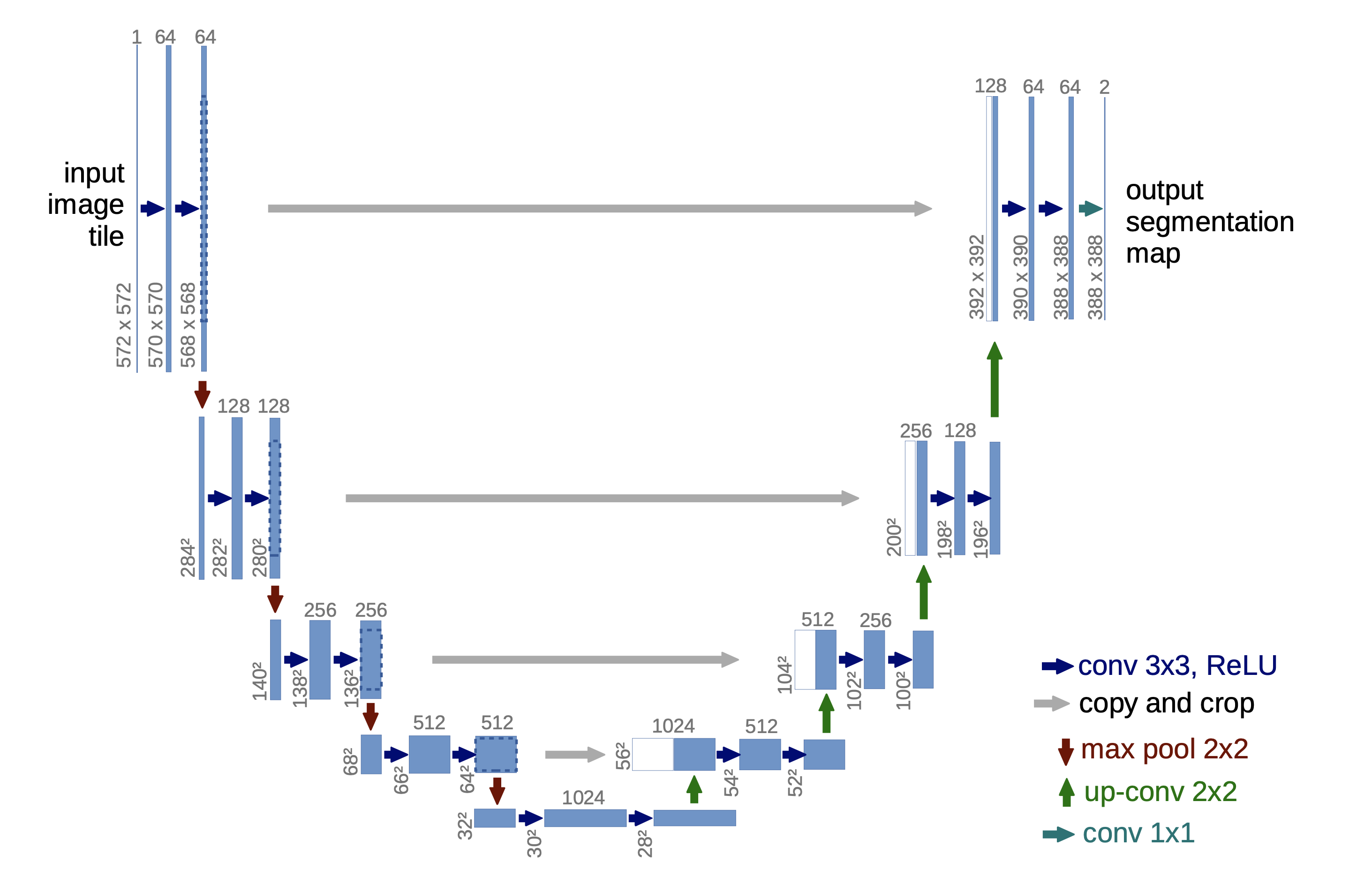
论文的说明如下,蓝色矩形表示多通道特征图,其顶部数字表示通道数,左侧数字表示图像长宽;白色矩形复制的特征图;箭头操作说明如图;
UNet是在FCN的基础上发展而来?|√,其结构可以分为两个主要部分:
- 压缩路径 |
Contracting path:用于提取图像的 高级语义信息,压缩了空间尺寸,但增加了通道数以增强了特征表达能力; - 扩展路径 |
Expanding Path:用于恢复图像空间尺寸,输出各像素分类结果以实现分割;
这种结构也可被视为encoder-decoder结构(Hinton, 2006),压缩路径 作为编码器提取多尺度语义特征,扩展路径 作为解码器将特征恢复到图像空间。
不同与FCN,UNet在上采样的过程中保留了特征图的大量通道数,将生成分类one-hot编码的步骤移至网络最后(最后的1x1 Conv2D),从而使得更多信息留向最终分割图像中。
需要注意的是,UNet在原论文中解决的是
pixel-wise的二分类问题(即分辨医学图像的前景与背景),若要将其用作多分类问题,可更改 损失函数 和Conv2D 1x1。
此外,两者在跳跃连接实现中也存在不同,UNet使用同层池化前特征图 拼接 | concatenation 上采样结果,再使用卷积层提取特征代替了FCN的两者直接 相加 | summation 处理。
针对跳跃连接的改进是一个很常见的创新点!
我们注意到在UNet结构图示中,UNet在跳跃连接中的复制操作实际上是在原特征图上截取一定空间范围内的图像,这对应了论文中提及的 重叠平铺 | overlap-tile 策略。
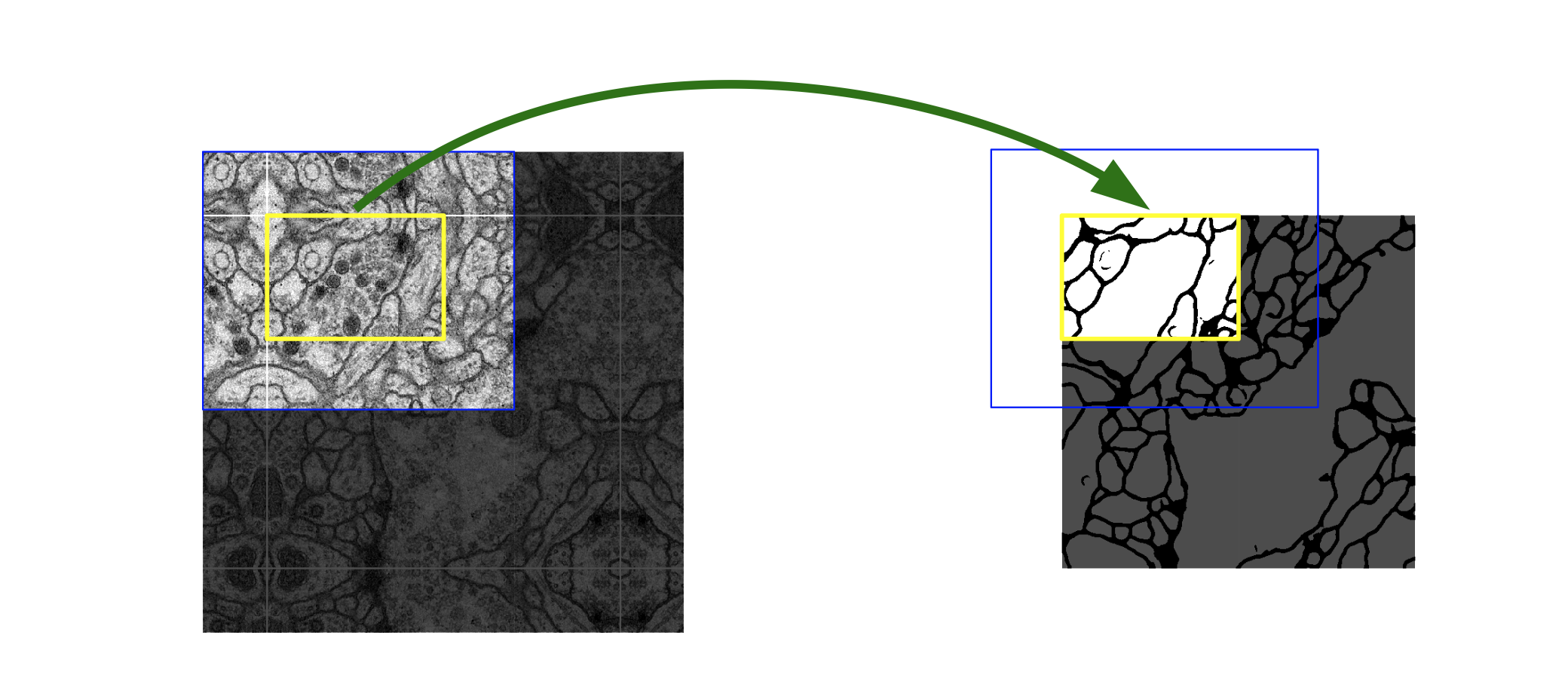
当UNet在处理大型图像的分割时,可以采用该策略,将待分割区域周围的内容一并用于模型训练与输入中,最终输出的分割结构会参考这些padding的信息,使UNet获得上下文信息以提高预测精度(当遇到周围部分无数据时,文中采用的是 镜像填补 | mirror padding 策略)。
3. 后续研究
UNet作为语义分割领域的经典结构,后续自然有许多研究者在其基础上进行创新,下面我们简要介绍一下相关改进网络。
UNet++
| 属性 | 详细信息 |
|---|---|
| 标题 | 🔬 Unet++: A nested u-net architecture for medical image segmentation 🔬 Unet++:一种用于医学图像分割的嵌套U-Net架构 |
| 会议 | 📚 Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support (DLMIA) 🏆 医学 |
| 日期 | ⏲️ 2018 |
| 作者 | 👨🔬 Zongwei Zhou |
在经典的U-Net架构中,解码器主要依赖于来自编码器最深层(即最小尺寸特征图)的信息来逐步恢复高分辨率特征图,而来自浅层的 跳跃连接 更多地作为辅助信息,用于补充细节。这意味着模型最终的表达能力在很大程度上取决于深层特征的提取效果。因此,当我们将U-Net应用于具体任务时,模型深度的设计就显得尤为关键。
而U-Net++在结构上引入了更密集的 跳跃连接,通过融合不同层次UNet编码器提取的特征图,使得每个解码器单元在恢复特征图尺寸时,能整合从不同感受野提取的图像特征信息,从而有效提升了特征表示能力与重建质量。UNet++的模型结构图如下:
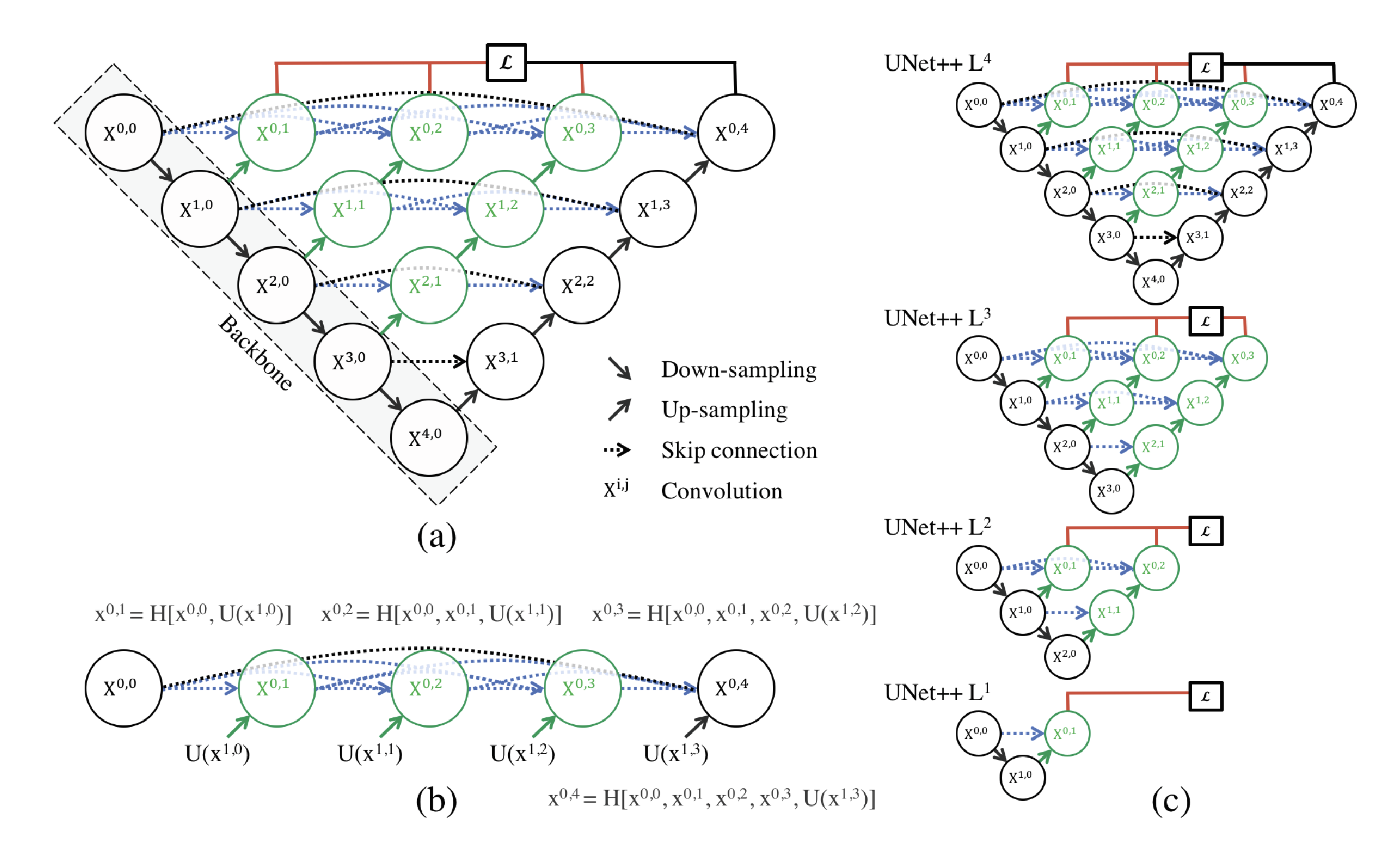
其中,图(a)是UNet++的总体架构图,本质上可以看作是由多层次的UNet子结构结合而成(例如节点 就共同构成一条U-Net路径),图(b)展示了第一层UNet++的详细结构,图(c)则是说明如果UNet++在训练时采用 深度监督 | deep supervision ,则在推理时进行剪枝操作。
最后,对于现在的我们而言(2025),相比了解模型结构,更有价值的是——从研究者的思路中汲取经验。其作者关于模型搭建的研究过程可以参考这两篇博客「UNet++解读 + 它是如何对UNet改进 + 作者的研究态度和方式 - 玖零猴」与「研习U-Net - 周纵苇」。
SETR
1. 论文信息
| 属性 | 详细信息 |
|---|---|
| 标题 | 🔬 Rethinking Semantic Segmentation From a Sequence-to-Sequence Perspective With Transformers 🔬 从序列到序列的视角重新思考语义分割:基于Transformers的方法 |
| 会议 | 📚 Conference on Computer Vision and Pattern Recognition (CVPR) 🏆 CCF-A |
| 日期 | ⏲️ 2021 |
| 作者 | 👨🔬 sixiao zheng |
SETR是将ViT(Transformer架构)用于语义分割领域的一次尝试。关于这篇论文的详细解读,大家可以去看看这篇博客「重新思考语义分割范式——SETR - 湃森」,这篇博客关于该论文的 模型结构 、相关工作 以及 背后争议 (创新性不足)的解答已经很详细了,在这里就不过多介绍了。下面我来着重介绍一下我对这篇论文的一些收获。
2. 论文内容
SETR实际上是探讨将ViT(Transformer架构)用于语义分割模型中的可行性,因此其encoder基本上是照搬了ViT的结构,然后论文还提出了三种decoder结构用于还原原图像尺寸的分割特征图。SETR的模型架构如下:
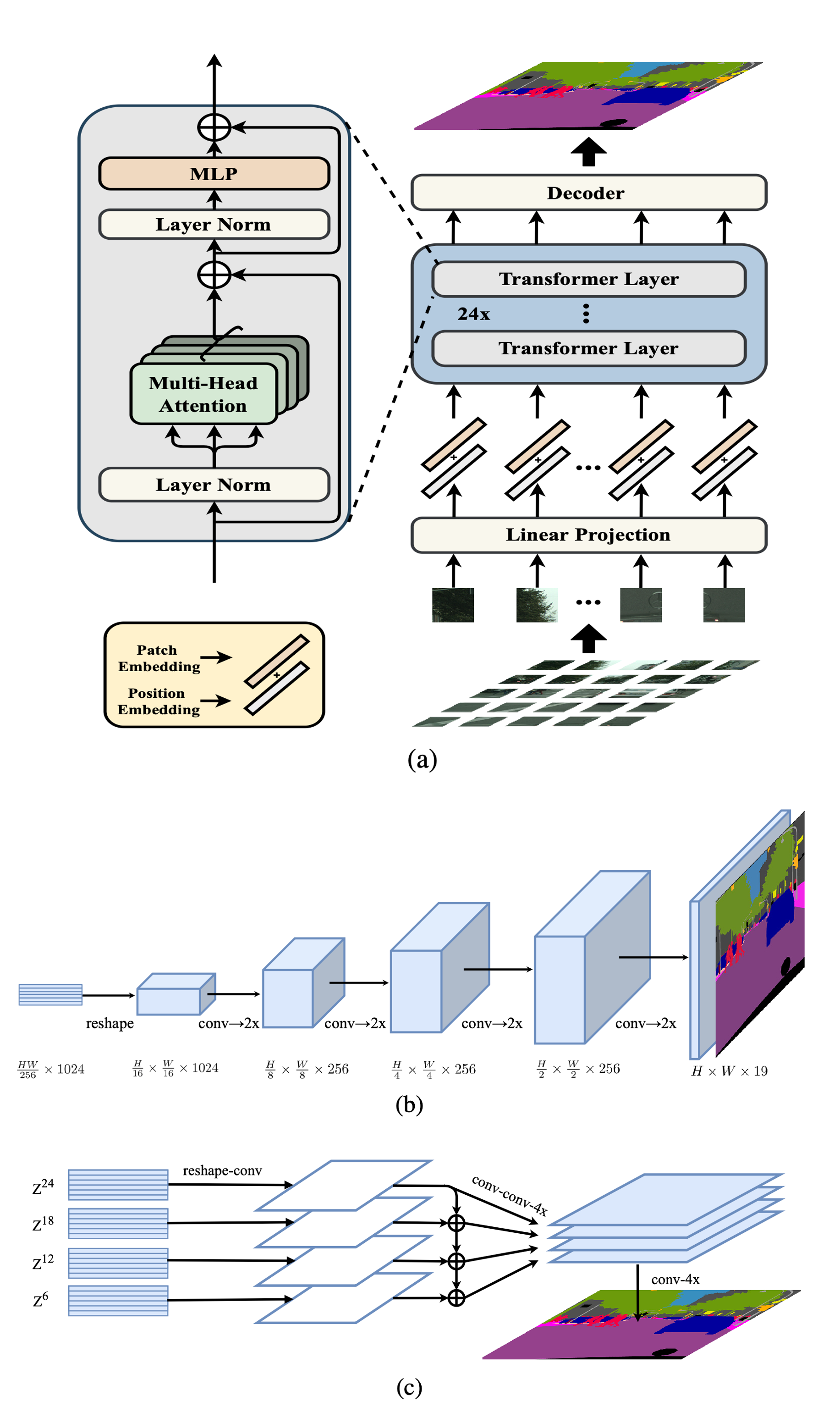
👜 模型结构
SETR的编码器与ViT的大致相同,也是先按patch做分割,然后以patch为单位进行序列化。由于Transformer架构只是给序列元素提取并添加全局注意力特征,不会改变输入序列的尺寸,因此SETR的编码器实际上输出还是按patch分割后长度的序列:
SETR原论文中, 即Transformer的 设置为 , 设置为 ,Transformer层数为 。因此其编码器最终输出尺寸为 的序列,下面我们来了解一下SETR原论文中为我们提供的三种解码器:
👶 SETR-Naive
SETR-Naive采用一层朴素上采样实现了从编码器输出特征图到原图尺寸的变换,其过程可用如下公式表示:
SETR-Naive的网络部分只是将原特征图维度降低到分类类别数的维度,以便与分类one-hot码计算 像素交叉熵 | Pixel-wise CE 损失函数。而其上采样则是使用双线性插值函数实现。此外,为了实现模型的分布式训练,SETR-Naive的 批标准化 | Batch Normalization 层使用的是Sync BN实现。乘此机会,我们在这里详细了解一下BN层和Pixel-wise CE损失函数。
BN层是用于加速神经网络训练、提升稳定性,其核心思想是对某一层的输入进行标准化处理:
BN层具体操作如下:我们假设有某一层(Layer)的批量输入数据为 ,其中 表示 batch size 。
BN层首先会计算当前批次数据的均值和方差:然后将原输入数据标准化为均值为0,方差为1的分布,即:
其中 是一个极小值,防止分母为 。
为了增强模型的表达能力,我们一般还会为
BN层添加两个可学习参数 和 调整标准化后的数据分布:
BN层有如下功能:
- 缓解梯度消失 / 爆炸:标准化使每一层输入分布更稳定,梯度变化更平缓。
- 加速收敛:允许使用更大的学习率,减少训练迭代次数。
- 降低初始化敏感度:对权重初始化的要求降低。
- 轻微正则化效果:批次统计的随机性引入微小噪声,减少过拟合。
而SETR-Naive用的Sync BN则是分布式训练场景下对BN的改进,核心是跨设备同步批次统计量。
在了解交叉熵前,我们需要先了解一下如下信息学概率:
🔹 自信息:衡量单个事件发生时所携带的信息量,事件发生的概率越低,其自信息越大。公式为:
其中, 表示某个事件,而 表示该事件发生的概率
🔹 熵:对随机变量不确定性的度量,即所有可能事件的自信息的期望。对于离散随机变量 ,其熵定义为:
熵值越大,变量的不确定性越高;当所有事件概率均等时,熵最大。
🔹 相对熵(KL散度):用于衡量两个概率分布 (真实分布)和 (预测分布)之间的差异。
公式为:
KL 散度越大,两个分布的差异越显著。其中, 便是交叉熵计算公式。
当我们用one-hot编码表示分类事件时,我们便可用 KL散度 描述真实事件和预测事件的分布差异,由于在训练时真实事件(即样本标注)已经确定,因此我们可以直接使用交叉熵计算误差。而 像素交叉熵 则是为整幅图像的像素点分别计算 交叉熵 ,然后取均值或求和作为最终损失值。
👨 SETR-PUP
SETR-PUP则是采用类似UNet的结构实现解码器,其使用渐进式上采样(Up-conv x2)分多层将输出特征图还原到原图大小,然后在最后次上采样中将通道数降至最终分类类别 。SETR-PUP选择两倍上采样可以有效避免引入过度的噪声。
👴 SETR-MLA
SETR-MLA采用类似 金字塔特征融合策略 的多层级特征融合方式,将SETR编码器不同层输出输出。其具体操作大致如下:
在SETR编码器中选取 个均匀分层(间隔为 )的输出特征序列 ,将其作为SETR-MLA解码器输入。需要注意的是,Transformer编码器各层输出尺寸保持一致,因此各输出序列尺寸为 ,在输入解码器前我们还需将其重塑为 形状:
其中, 的 表示解码器的输入, 表示输入输出对应的 流 | stream (分支)。
接下来,SETR-MLA对每个分支输入数据都使用一个三层网络(1x1→3x3→3x3)处理:
第一层使用
Conv2D 1x1将低输入特征图通道数(),得到 。MLA使用 自顶向下 |
top-down的相加聚合方式融合不同层次的特征图:MLA使用一层
Conv2D 3x3融合相加聚合后的特征图(),然后加上一层Conv2D 3x3将特征图通道数减半,得到 。经过上述操作后,MLA先做
x4()的双线性上采样放大特征图尺寸,在将所有分支特征图 拼接 |concatenate到一起,得到 。最后,MLA使用
Conv2D 1x1将特征图尺寸将为待分类数 得到logits,然后再使用x4()的双线性上采样将特征图还原到原图大小。
借物表
| 参考 | 说明 |
|---|---|
| 全卷积网络FCN详解 - ZOMI酱 | 知乎文章|FCN参考 |
| FCN详解 - 酿久诗 | CSDN文章|FCN参考 |
| 精读论文U-Net - 菜菜的小孙同学 | CSDN文章|UNet参考 |
| UNet++解读 + 它是如何对UNet改进 + 作者的研究态度和方式 - 玖零猴 | 知乎文章|UNet++参考 |
| 研习U-Net - 周纵苇 | 知乎文章|UNet++参考 |
| 重新思考语义分割范式——SETR - 湃森 | 知乎文章|SETR参考 |